Question

【题目】在直角坐标系中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为，过点的直线l的参数方程为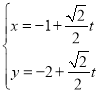（t为参数），l与C交于A，B两点．

（1）求C的直角坐标方程和l的普通方程；

（2）若，，成等比数列，求a的值．

Answer 1

【答案】（1）直线l的普通方程为，曲线C的直角坐标方程为；

（2）．

【解析】

（1）由，两边同乘ρ，由此能求出C的直角坐标方程;将直线l的参数方程消去参数t，能求出直线I的普通方程；

（2）把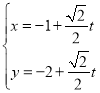代入，根据根与系数的关系及参数的几何意义即可求解.

（1）由，两边同乘ρ，得，

化为普通方程为，

将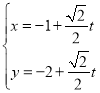消去参数t，得直线l的普通方程为．

（2）把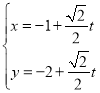代入，整理得，

∴，，

由，得或，

∵，

∴，

∵，，成等比数列，

∴，

由t的几何意义得，即，

∴，即，

解得，又，

∴．