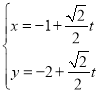题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)a≥-2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为![]() ,其中
,其中![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题本题主要考查函数的单调性、函数的最值、导数等基础知识,意在考查考生的运算求解能力、推理论证能能力以及分类讨论思想和等价转化思想的应用.第一问,先确定![]() 的解析式,求出函数
的解析式,求出函数![]() 的定义域,对
的定义域,对![]() 求导,此题需讨论
求导,此题需讨论![]() 的判别式,来决定
的判别式,来决定![]() 是否有根,利用
是否有根,利用![]() 求函数的增区间,
求函数的增区间,![]() 求函数的减区间;第二问,先确定
求函数的减区间;第二问,先确定![]() 解析式,确定函数的定义域,先对函数
解析式,确定函数的定义域,先对函数![]() 求导,求出
求导,求出![]() 的两根,即
的两根,即![]() ,而利用韦达定理,得到
,而利用韦达定理,得到![]() ,
,![]() ,即得到
,即得到![]() ,
,![]() 代入到
代入到![]() 中,要求
中,要求![]() ,则构造函数
,则构造函数![]() ,求出
,求出![]() 的最小值即可,对
的最小值即可,对![]() 求导,判断函数
求导,判断函数![]() 的单调性,求出函数
的单调性,求出函数![]() 的最小值即为所求.
的最小值即为所求.
试题解析:(1)由题意![]() ,其定义域为
,其定义域为![]() ,则
,则![]() ,2分
,2分
对于![]() ,有
,有![]() .
.
①当![]() 时,
时,![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]() ;
;
②当![]() 时,
时,![]() 的两根为
的两根为![]() ,
,![]()
∴![]() 的单调增区间为
的单调增区间为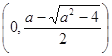 和
和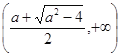 ,
,
![]() 的单调减区间为
的单调减区间为 .
.
综上:当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时,
时,![]() 的单调增区间为
的单调增区间为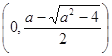 和
和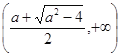 ,
,
![]() 的单调减区间为
的单调减区间为 . 6分
. 6分
(2)对![]() ,其定义域为
,其定义域为![]() .
.
求导得,![]() ,
,
由题![]() 两根分别为
两根分别为![]() ,
,![]() ,则有
,则有![]() ,
,![]() , 8分
, 8分
∴![]() ,从而有
,从而有![]()
![]() , 10分
, 10分
![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
,
∴![]() . 12分
. 12分

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目