题目内容
【题目】节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮的时候相差不超过2秒的概率是（ ）
A.
B.
C.
D.
【答案】C
【解析】解：设两串彩灯第一次闪亮的时刻分别为x，y，
由题意可得0≤x≤4，0≤y≤4，
它们第一次闪亮的时候相差不超过2秒，则|x﹣y|≤2，
由几何概型可得所求概率为上述两平面区域的面积之比，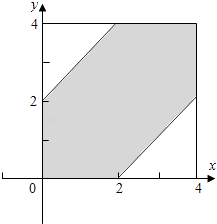
由图可知所求的概率为： 
= 
故选C
设两串彩灯第一次闪亮的时刻分别为x，y，由题意可得0≤x≤4，0≤y≤4，要满足条件须|x﹣y|≤2，作出其对应的平面区域，由几何概型可得答案．
【题目】某学校课题组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级
名学生某次考试成绩（百分制）如下表所示：
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 |
序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
数学成绩 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
物理成绩 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若数学成绩
分以上为优秀，物理成绩
分（含分）以上为优秀.
（Ⅰ）根据上表完成下面的
列联表：
数学成绩优秀 | 数学成绩不优秀 | 合计 | |
物理成绩优秀 | |||
物理成绩不优秀 | 12 | ||
合计 | 20 |
（Ⅱ）根据题（Ⅰ）中表格的数据计算，有多少的把握认为学生的数学成绩与物理成绩之间有关系？
（Ⅲ）若按下面的方法从这人中抽取
人来了解有关情况：将一个标有数字，
，
，
，
，
的正六面体骰子连续投掷两次，记朝上的两个数字的乘积为被抽取人的序号，试求：抽到
号的概率.
参考数据公式：①独立性检验临界值表
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
②独立性检验随机变量
值的计算公式：
.
【题目】为推行“新课堂”教学法, 某化学老师分别用传统教学和“新课堂”两种不同的教学方式, 在甲、乙两个平行班进行教学实验, 为了解教学效果, 期中考试后, 分别从两个班级中各随机抽取20名学生的成绩进行统计, 作出的茎叶图如下图, 记成绩不低于70分者为“成绩优良”.
(1) 分别计算甲、乙两班20个样本中, 化学成绩前十的平均分, 并据此判断哪种教学方式的教学效果更佳;
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总 计 |
（2）由以上统计数据填写下面2×2列联表,是否有95%的把握认为“成绩优良与教学方式关”?
| 0.05 | 0.010 |
| 3.841 | 6.635 |
