题目内容
已知数列{an}的通项公式是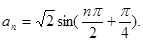
设其前n项和为Sn，则S12 .
0
解析试题分析：数列{an}的周期为T=4，而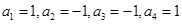
，所以
.
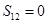考点：1、三角函数值的运算；2、数列的周期性；3、数列的求和.
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
小学同步三练核心密卷系列答案题目内容
已知数列{an}的通项公式是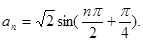设其前n项和为Sn，则S12 .
0
解析试题分析：数列{an}的周期为T=4，而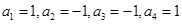，所以.
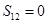考点：1、三角函数值的运算；2、数列的周期性；3、数列的求和.
小学同步三练核心密卷系列答案
，定义Hn＝
为
，则数列
具有如下性质:①
为正整数；②对于任意的正整数
,当
为偶数时,
;当
.在数列
时，
，当
时，
（
，
），则首项
表示）
中，若
，
，则该数列的通项
________________.
（
），数列
满足
，
，
.则
与
中，较大的是________；
的大小关系是_____________．
，各项均为正数的数列
满足
，若
，则
.
}满足
，则
的值为 ．
中有性质： 
（
），类比这一性质，试在等比数列
中写出一个结论： .