题目内容
设向量 ,
,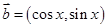 ,
,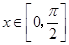 .
.
(1)若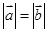 ,求
,求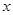 的值;
的值;
(2)设函数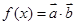 ,求
,求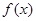 的最大值.
的最大值.
(1)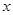 的值为
的值为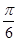 ;(2)
;(2)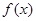 的最大值为
的最大值为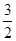 .
.
解析试题分析:(1)去除向量的包装外衣,转化为由三角函数值求对应的角的值;(2)去除向量的包装外衣,转化为形如: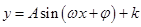 三角函数最值,但一定要关注自变量
三角函数最值,但一定要关注自变量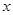 的范围.另外三角函数与代数函数一个很大的区别就是一般先要处理三角函数表达式,处理的结果之一就是转化为形如:
的范围.另外三角函数与代数函数一个很大的区别就是一般先要处理三角函数表达式,处理的结果之一就是转化为形如: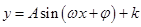 ,这一点很重要.
,这一点很重要.
试题解析:(1)由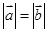 得
得
 ,即
,即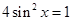 ,
,
又∵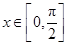 ,∴
,∴ ,从而
,从而 . (5分)
. (5分)
(2)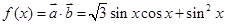
 ,
,
又∵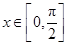 ,∴
,∴ ,即有
,即有 ,所以
,所以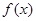 的最大值为
的最大值为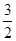 . (14分)
. (14分)
考点:1.平面向量基础知识;2.三角函数式的恒等变形;3.三角函数的图形与性质.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 的方向向量为
的方向向量为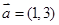 ,且过点
,且过点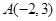 ,将直线
,将直线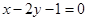 绕着它与x轴的交点B按逆时针方向旋转一个锐角
绕着它与x轴的交点B按逆时针方向旋转一个锐角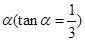 得到直线
得到直线 ,直线
,直线 :
: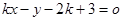 .(k
.(k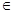 R).
R).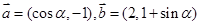 ,且
,且
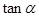 的值
的值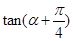 的值
的值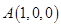 ,
, ,
,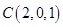 .
.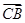 与
与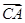 的夹角;
的夹角;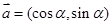 ,
,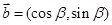 ,其中
,其中
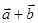 与
与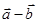 互相垂直;
互相垂直;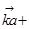
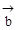 与
与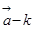
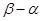 的值(
的值(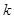 为非零的常数) .
为非零的常数) .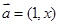 ,
, 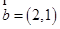 满足条件
满足条件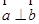 ,则
,则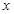 =__________
=__________ 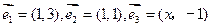 ,且
,且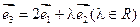 ,则实数
,则实数 的值是 .
的值是 .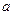 >0,若平面内三点A(1,-
>0,若平面内三点A(1,-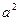 ),C(3,
),C(3,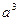 )共线,则
)共线,则