题目内容
已知直线 的方向向量为
的方向向量为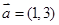 ,且过点
,且过点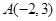 ,将直线
,将直线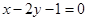 绕着它与x轴的交点B按逆时针方向旋转一个锐角
绕着它与x轴的交点B按逆时针方向旋转一个锐角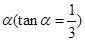 得到直线
得到直线 ,直线
,直线 :
: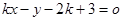 .(k
.(k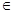 R).
R).
(1)求直线 和直线
和直线 的方程;
的方程;
(2)当直线 ,
, ,
, 所围成的三角形的面积为3时,求直线
所围成的三角形的面积为3时,求直线 的方程。
的方程。
(1)直线 方程为:
方程为: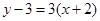 ,
, 的方程为x-y-1=0;(2)直线
的方程为x-y-1=0;(2)直线 的方程为:7x-4y-2=0或13x-10y+4=0.
的方程为:7x-4y-2=0或13x-10y+4=0.
解析试题分析:(1)本小题由已知条件利用点斜式方程能求出直线 的方程(其中方向向量可用以求其斜率),设直线
的方程(其中方向向量可用以求其斜率),设直线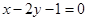 的倾斜角为
的倾斜角为 ,则
,则 的斜率为
的斜率为 ,从而可求得
,从而可求得 的方程;(2)可知直线
的方程;(2)可知直线 过定点M(2,3),由
过定点M(2,3),由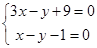 ,得直线
,得直线 与
与 的交点为C(-5,-6),点A到
的交点为C(-5,-6),点A到 的距离为
的距离为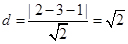 ,联立
,联立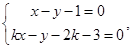 得直线
得直线 ,
, 的交点B(
的交点B( ),又因为直线
),又因为直线 ,
, ,
, 所围成的三角形的面积为3,所以有
所围成的三角形的面积为3,所以有 ,再利用两点间的距离公式求得k的值,即可求得
,再利用两点间的距离公式求得k的值,即可求得 的方程.
的方程.
试题解析:(1)因为直线 的方向向量为
的方向向量为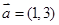 ,且过点
,且过点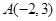 ,所以直线
,所以直线 方程为:
方程为: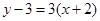 ,整理,得
,整理,得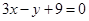 .将直线
.将直线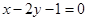 绕着它与x轴的交点B按逆时针方向旋转一个锐角
绕着它与x轴的交点B按逆时针方向旋转一个锐角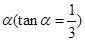 得到直线
得到直线 ,设直线
,设直线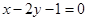 的倾斜角为
的倾斜角为 ,且有B(1,0),则
,且有B(1,0),则 的斜率为
的斜率为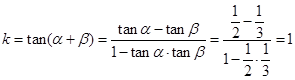 ,所以
,所以 的方程为:y=x-1,整理得x-y-1=0.
的方程为:y=x-1,整理得x-y-1=0.
(2)因为直线 :
: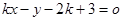 ,即为(x-2)k+(3-y)=0,所以
,即为(x-2)k+(3-y)=0,所以 过定点M(2,3),由
过定点M(2,3),由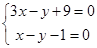 ,得直线
,得直线 与
与 的交点为C(-5,-6),点A到
的交点为C(-5,-6),点A到 的距离为
的距离为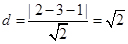 ,联立
,联立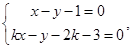 得直线
得直线 ,
, 的交点B(
的交点B( ),又因为直线
),又因为直线 ,
, ,
, 所围成的三角形的面积为3,所以有
所围成的三角形的面积为3,所以有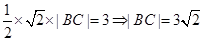 ,则
,则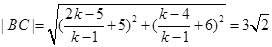 ,解得
,解得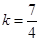 或
或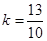 ,所以所求直线
,所以所求直线 的方程为:7x-4y-2=0或13x-10y+4=0.
的方程为:7x-4y-2=0或13x-10y+4=0.
考点:直线的点斜式,斜截式方程,两直线求交点,两角和的正切公式,点到直线的距离公式,两点间的距离公式,三角形的面积公式.

练习册系列答案
相关题目
 ,
,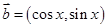 ,
,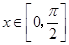 .
.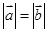 ,求
,求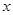 的值;
的值;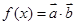 ,求
,求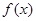 的最大值.
的最大值.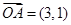 ,
,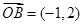 ,向量
,向量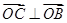 ,
,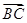 ∥
∥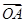 ,又
,又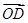 +
+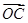 ,求
,求 =3
=3 ,
, =2
=2 ,求点M、N及
,求点M、N及 的坐标.
的坐标. 、
、 、
、 两两所成的角相等,并且|
两两所成的角相等,并且|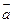 与
与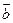 满足:
满足: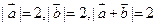 ,则
,则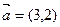 ,
,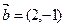 ,若
,若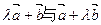 平行,则λ= .
平行,则λ= . //
//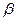 ,在
,在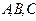 ,在
,在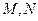 ,又
,又 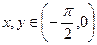 且
且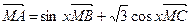 ,
, 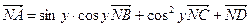 ,则
,则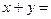 .
.