题目内容
【题目】已知椭圆C: ![]() 的右顶点A(2,0),且过点
的右顶点A(2,0),且过点 ![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(1,0)且斜率为k1(k1≠0)的直线l于椭圆C相交于E,F两点,直线AE,AF分别交直线x=3于M,N两点,线段MN的中点为P,记直线PB的斜率为k2 , 求证:k1k2为定值.
【答案】解:(Ⅰ)由题意可得a=2, ![]() +
+ ![]() =1,
=1,
a2﹣b2=c2 ,
解得b=1,
即有椭圆方程为 ![]() +y2=1;
+y2=1;
(Ⅱ)证明:设过点B(1,0)的直线l方程为:y=k1(x﹣1),
由 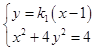 ,
,
可得:(4k12+1)x2﹣8k12x+4k12﹣4=0,
因为点B(1,0)在椭圆内,所以直线l和椭圆都相交,
即△>0恒成立.
设点E(x1 , y1),F(x2 , y2),
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() .
.
因为直线AE的方程为:y= ![]() (x﹣2),
(x﹣2),
直线AF的方程为:y= ![]() (x﹣2),
(x﹣2),
令x=3,得M(3, ![]() ),N(3,
),N(3, ![]() ),
),
所以点P的坐标(3, ![]() (
( ![]() +
+ ![]() )).
)).
直线PB的斜率为k2= 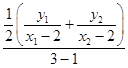 =
= ![]() (
( ![]() +
+ ![]() )
)
= ![]()
![]() =
= ![]()
![]()
= ![]()
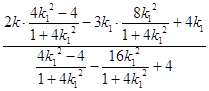 =﹣
=﹣ ![]() .
.
所以k1k2为定值﹣ ![]() .
.
【解析】(Ⅰ)由题意可得a=2,代入点 ![]() ,解方程可得椭圆方程;(Ⅱ)设过点B(1,0)的直线l方程为:y=k(x﹣1),由
,解方程可得椭圆方程;(Ⅱ)设过点B(1,0)的直线l方程为:y=k(x﹣1),由 ![]() ,可得(4k12+1)x2﹣8k12x+4k12﹣4=0,由已知条件利用韦达定理推导出直线PB的斜率k2=﹣
,可得(4k12+1)x2﹣8k12x+4k12﹣4=0,由已知条件利用韦达定理推导出直线PB的斜率k2=﹣ ![]() ,由此能证明kk′为定值﹣
,由此能证明kk′为定值﹣ ![]() .
.

【题目】某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如图.记成绩不低于90分者为“成绩优秀”.

(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个均“成绩优秀”的概率;
(2)由以上统计数据作出列联表,并判断能否在犯错误的概率不超过0.1的前提下认为:“成绩优秀”与教学方式有关.
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考公式:![]()
![]()
【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响,部分统计数据如下:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 |
|
| |
学习成绩不优秀 |
|
| |
合计 |
(1)根据以上统计数据,你是否有![]() 的把握认为使用智能手机对学习有影响?
的把握认为使用智能手机对学习有影响?
(2)为进一步了解学生对智能手机的使用习惯,现从全校使用智能手机的高中生中(人数很多)随机抽取 ![]() 人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()



