题目内容
【题目】如图,A、B、C为⊙O上三点,B为 ![]() 的中点,P为AC延长线上一点,PQ与⊙O相切于点Q,BQ与AC相交于点D.
的中点,P为AC延长线上一点,PQ与⊙O相切于点Q,BQ与AC相交于点D.
(Ⅰ)证明:△DPQ为等腰三角形;
(Ⅱ)若PC=1,AD=PD,求BDQD的值.
【答案】证明:(Ⅰ)连接CQ,BC,AB,
因为PQ是圆O的切线,所以∠PQC=∠CBD,
因为B为 ![]() 的中点,所以∠CQB=∠ACB,
的中点,所以∠CQB=∠ACB,
所以∠PQC+∠CQB=∠CBD+∠ACB,
即∠PQD=∠CDQ,
故△DPQ为等腰三角形.
(Ⅱ)解:设CD=t,则PD=PQ=1+t,PA=2+2t,
由PQ2=PCPA得t=1,
所以CD=1,AD=PD=2,
所以BDQD=CDAD=2.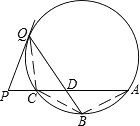
【解析】(Ⅰ)连接CQ,BC,AB,证明∠PQD=∠CDQ,即可证明PD=PQ;(Ⅱ)利用切割线定理,求出CD=1,AD=PD=2,即可求BDQD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响,部分统计数据如下:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 |
|
| |
学习成绩不优秀 |
|
| |
合计 |
(1)根据以上统计数据,你是否有![]() 的把握认为使用智能手机对学习有影响?
的把握认为使用智能手机对学习有影响?
(2)为进一步了解学生对智能手机的使用习惯,现从全校使用智能手机的高中生中(人数很多)随机抽取 ![]() 人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()