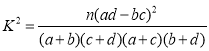题目内容
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处切线与坐标轴围成的三角形面积为
处切线与坐标轴围成的三角形面积为![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() 或
或![]() ;(2)见解析
;(2)见解析
【解析】
(1)利用导函数求出曲线![]() 在
在![]() 处切线,表示出切线与坐标轴围成三角形面积即可求解;
处切线,表示出切线与坐标轴围成三角形面积即可求解;
(2)需证明的不等式通过作差转化成证明![]() ,利用导函数单调性求出最小值即可得证.
,利用导函数单调性求出最小值即可得证.
(1)![]() ,则
,则![]() 为切线斜率.
为切线斜率.
又![]() ,∴切点为
,∴切点为![]() .∴曲线在
.∴曲线在![]() 处切成方程为
处切成方程为![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() (易知
(易知![]() )
)
则切线与坐标轴围成三角形面积为![]() .
.
∴![]() 得
得![]() .
.
所以![]() 或
或![]() .
.
(2)法一:![]() 时,
时,![]()
要证的不等式为![]() ,即
,即![]() .
.
令![]() ,则
,则![]() .
.
易知![]() 递增,
递增,![]() ,
,![]() ,∴
,∴![]() 仅有一解
仅有一解![]() 且
且![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,
,![]() 递减;当
递减;当![]() 时,
时,![]() ,
,![]() 递增.
递增.
从而![]() 最小值为
最小值为![]() ∴
∴![]() ,故原不等式成立.
,故原不等式成立.
法二:![]() 时,要证的不等式为
时,要证的不等式为![]() .令
.令![]() ,则
,则![]() .
.
故问题化为证不等式![]() 恒成立.
恒成立.![]() 时,
时,![]()
令![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,![]() 递减;
递减;
当![]() 时,
时,![]() ,
,![]() 递增.∴
递增.∴![]() ,从而原不等式成立.
,从而原不等式成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了拓展城市的旅游业,实现不同市区间的物资交流,政府决定在![]() 市与
市与![]() 市之间建一条直达公路,中间设有至少8个的偶数个十字路口,记为
市之间建一条直达公路,中间设有至少8个的偶数个十字路口,记为![]() ,现规划在每个路口处种植一颗杨树或者木棉树,且种植每种树木的概率均为
,现规划在每个路口处种植一颗杨树或者木棉树,且种植每种树木的概率均为![]() .
.
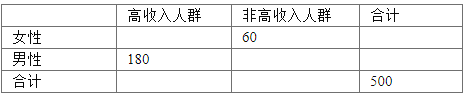
(1)现征求两市居民的种植意见,看看哪一种植物更受欢迎,得到的数据如下所示:
A市居民 | B市居民 | |
喜欢杨树 | 300 | 200 |
喜欢木棉树 | 250 | 250 |
是否有![]() 的把握认为喜欢树木的种类与居民所在的城市具有相关性;
的把握认为喜欢树木的种类与居民所在的城市具有相关性;
(2)若从所有的路口中随机抽取4个路口,恰有![]() 个路口种植杨树,求
个路口种植杨树,求![]() 的分布列以及数学期望;
的分布列以及数学期望;
(3)在所有的路口种植完成后,选取3个种植同一种树的路口,记总的选取方法数为![]() ,求证:
,求证:![]() .
.
附: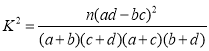
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |