��Ŀ����
����Ŀ��Ϊ����չ���е�����ҵ��ʵ�ֲ�ͬ����������ʽ���������������![]() ����
����![]() ��֮�佨һ��ֱ�﹫·���м���������8����ż����ʮ��·�ڣ���Ϊ
��֮�佨һ��ֱ�﹫·���м���������8����ż����ʮ��·�ڣ���Ϊ![]() ���ֹ滮��ÿ��·�ڴ���ֲһ����������ľ����������ֲÿ����ľ�ĸ��ʾ�Ϊ
���ֹ滮��ÿ��·�ڴ���ֲһ����������ľ����������ֲÿ����ľ�ĸ��ʾ�Ϊ![]() .
.
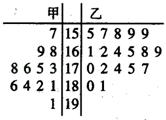
��1�����������о������ֲ�����������һ��ֲ����ܻ�ӭ���õ�������������ʾ��
A��� | B��� | |
ϲ������ | 300 | 200 |
ϲ��ľ���� | 250 | 250 |
�Ƿ���![]() �İ�����Ϊϲ����ľ��������������ڵij��о�������ԣ�
�İ�����Ϊϲ����ľ��������������ڵij��о�������ԣ�
��2���������е�·���������ȡ4��·�ڣ�ǡ��![]() ��·����ֲ��������
��·����ֲ��������![]() �ķֲ����Լ���ѧ������
�ķֲ����Լ���ѧ������
��3�������е�·����ֲ��ɺ�ѡȡ3����ֲͬһ������·�ڣ����ܵ�ѡȡ������Ϊ![]() ����֤��
����֤��![]() .
.
����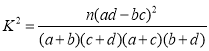
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
���𰸡���1��û�У�2���ֲ��м�������![]() ��3��֤��������
��3��֤��������
��������
��1�����ݹ�ʽ���㿨��ֵ���ٶ�Ӧ��ֵ���ж�..
��2���������⣬�������![]() �Ŀ���ȡֵΪ0��1��2��3��4���ֱ���ø��ʣ�д���ֲ��У�����������ʽ��ֵ.
�Ŀ���ȡֵΪ0��1��2��3��4���ֱ���ø��ʣ�д���ֲ��У�����������ʽ��ֵ.
��3����Ϊ����8����ż����ʮ��·�ڣ�����![]() ����
����![]() .Ҫ֤
.Ҫ֤![]() ����֤
����֤![]() �������������ʽ����֤
�������������ʽ����֤![]() ����֪��
����֪��![]() .����.��
.����.��![]() ��·������
��·������![]() ��·����ֲ����������������ۢٵ�
��·����ֲ����������������ۢٵ�![]() ʱ����
ʱ����![]() ��֤.�ڵ�
��֤.�ڵ�![]() ʱ����
ʱ����![]() ��֤.�۵�
��֤.�۵�![]() ʱ��
ʱ��![]() ����
����![]() ������֤��
������֤��![]() ʱ��
ʱ��![]() ȡ����Сֵ����.
ȡ����Сֵ����.
��1������ʵ���У�![]() ��
��
��û��99.9%�İ�����Ϊϲ����ľ��������������ڵij��о��������.
��2�������⣬![]() �Ŀ���ȡֵΪ0��1��2��3��4��
�Ŀ���ȡֵΪ0��1��2��3��4��
��![]() ��
��![]() ��
��
![]()
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
��![]() .
.
��3����![]() ����
����![]() .Ҫ֤
.Ҫ֤![]() ����֤
����֤![]() ��
��
����֤����������![]() ����
����![]() .
.
֤������Ϊ![]() ������
������![]() .
.
��![]() ��·������
��·������![]() ��·����ֲ������
��·����ֲ������
�ٵ�![]() ʱ��
ʱ��
![]() ��
��
��Ϊ![]() ������
������![]() ��
��
����![]() .
.
�ڵ�![]() ʱ��
ʱ��![]() ��ͬ�Ͽɵ�
��ͬ�Ͽɵ�![]()
�۵�![]() ʱ��
ʱ��![]() ����
����![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��Ȼ![]() ����
����![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ��
��
���![]() ����
����![]() .
.
���ϣ�![]() ����
����![]() .
.

 �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�