题目内容
10.作出下列函数的图象(1)y=a|x|(0<a<1)
(2)y=3${\;}^{lo{g}_{3}|x|}$
(3)y=log2|x-1|
(4)y=x2-2|x|-1.
分析 根据指数函数,对数函数,二次函数的图象,结合函数的平移变换和对折变换法则,可得各个函数的图象.
解答 解(1)函数y=a|x|(0<a<1)的图象由函数y=ax(0<a<1)的图象作一次横向对折变换得到,
其图象如下图所示: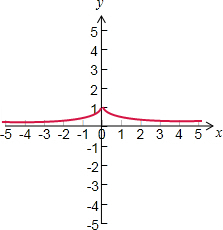
(2)函数y=3${\;}^{lo{g}_{3}|x|}$=|x|(x≠0)的图象由函数y=x(x≠0)的图象作一次横向对折变换得到,
其图象如下图所示:
(3)函数y=log2|x-1|的图象由函数y=log2x的图象作一次横向对折变换后,再向右平移一个单位得到,
其图象如下图所示: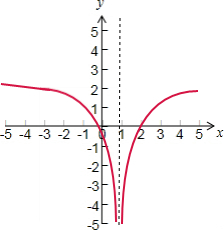
(4)函数y=x2-2|x|-1的图象由函数y=x2-2x-1的图象作一次横向对折变换得到,
其图象如下图所示: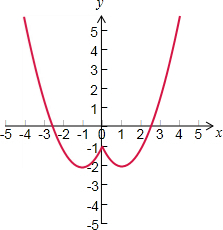
点评 本题考查的知识点是函数的图象,熟练掌握各种基本初等函数的图象和性质,及函数图象的变换法则,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知点M是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左支上一点,F是其右焦点,若$\overrightarrow{OP}$•$\overrightarrow{MF}$=0,且$\overrightarrow{PM}$=-$\frac{1}{2}$$\overrightarrow{MF}$,当|$\overrightarrow{OP}$|=$\frac{1}{2}$a时,该双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
15.若0<α<$\frac{π}{2}$,0<β$<\frac{π}{2}$,且tanα=$\frac{1}{7}$,tanβ=$\frac{3}{4}$,求证:α+β=$\frac{π}{4}$.
17.关于x的不等式x2-bx+c<0的解集为(-1,2),则方程x2-bx+2c=0的两根之积为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |