题目内容
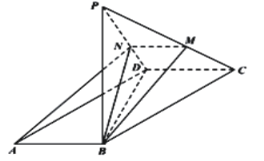
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
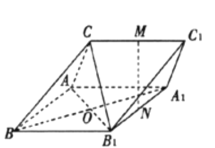
(1)证明:直线![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() ,
,![]() ,
,![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)设![]() 与
与![]() 交于点
交于点![]() ,通过证明
,通过证明![]() 是平行四边形证得
是平行四边形证得![]() ,得线面平行;
,得线面平行;
(2)证明![]() 两两垂直,然后以
两两垂直,然后以![]() 为
为![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,写出各点坐标,求出两平面的法向量,利用法向量夹角的余弦得二面角的余弦.
,写出各点坐标,求出两平面的法向量,利用法向量夹角的余弦得二面角的余弦.
证明:(1)设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,
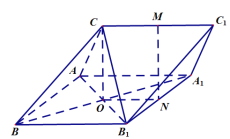
因为四边形![]() 是平行四边形,所以
是平行四边形,所以![]() 是
是![]() 的中点,
的中点,
![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,![]() .
.
又因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,![]() .
.
所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() .又因为
.又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.
(2)因为![]() ,所以平行四边形
,所以平行四边形![]() 是菱形,所以
是菱形,所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
又![]() ,且
,且![]() 是
是![]() 的中点,所以
的中点,所以![]() .又因为
.又因为![]() ,
,
所以![]() ,
,
所以![]() ,故
,故![]() ,从而
,从而![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图空间直角坐标系
轴建立如图空间直角坐标系![]() ,
,
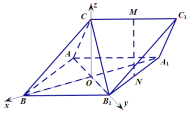
设![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() 是等边三角形,所以
是等边三角形,所以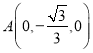 ,
,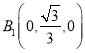 ,
,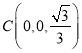 ,
,![]() .
.
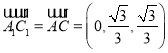 ,
,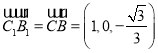 .
.
因为![]() ,
,![]() ,
,![]() 两两垂直,所以
两两垂直,所以![]() 平面
平面![]() ,
,
所以![]() 是平面
是平面![]() 的一个法向量;
的一个法向量;
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
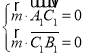 ,即
,即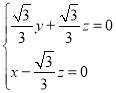 ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值为
所成的角(锐角)的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润增长 | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
(1)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程(结果保留两位小数);
的回归直线方程(结果保留两位小数);
(2)现从2012—2018年这7年中抽出三年进行调查,记![]() 年利润增长-投资金额,设这三年中
年利润增长-投资金额,设这三年中![]() (万元)的年份数为
(万元)的年份数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考公式: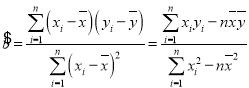 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.