题目内容
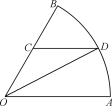
【题目】如图,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 是椭圆右顶点,已知直线
是椭圆右顶点,已知直线![]() 的斜率为
的斜率为![]() ,
,![]() 的外接圆半径为
的外接圆半径为![]() .
.

(1)求椭圆的方程;
(2)若椭圆上有两点![]() ,使
,使![]() 的平分线垂直
的平分线垂直![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)设![]() ,
,![]() ,根据直线
,根据直线![]() 的斜率为
的斜率为![]() ,可得
,可得![]() ,再利用
,再利用![]() ,即可得
,即可得![]() 是直角三角形,从而可求出
是直角三角形,从而可求出![]() 的长,再结合
的长,再结合![]() ,可求出
,可求出![]() 的长,进而求出
的长,进而求出![]() 及点
及点![]() 的坐标,将
的坐标,将![]() 的坐标代入椭圆的方程即可求出
的坐标代入椭圆的方程即可求出![]() ;
;
(2) 由(1)知![]() ,由
,由![]() 的平分线垂直
的平分线垂直![]() 知直线
知直线![]() 与
与![]() 关于
关于![]() 对称,因此可设
对称,因此可设![]() 的斜率为
的斜率为![]() ,则
,则![]() 的斜率为
的斜率为![]() ,将直线分别与椭圆联立方程组,利用两根之积,求出
,将直线分别与椭圆联立方程组,利用两根之积,求出![]() 的坐标,从而可求出直线
的坐标,从而可求出直线![]() 的斜率,再利用弦长公式求出
的斜率,再利用弦长公式求出![]() 即可求出
即可求出![]() ,进而求出直线
,进而求出直线![]() 的方程.
的方程.
(1)连结![]() ,设
,设![]() ,
,![]() ,所以直线
,所以直线![]() 的斜率
的斜率![]() ,所以
,所以![]() ,
,
所以![]() ,由椭圆的对称性可知
,由椭圆的对称性可知![]() ,所以
,所以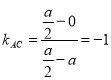 ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() 是直角三角形,
是直角三角形,
故![]() 的外接圆半径
的外接圆半径![]() ,所以
,所以![]() ,
,
因为直线![]() 的方程为
的方程为![]() ,所以直线
,所以直线![]() 的倾斜角
的倾斜角![]() ,
,
所以![]() ,所以在
,所以在![]() 中,
中,![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,代入椭圆的方程可得
,代入椭圆的方程可得![]() ,
,
所以![]() ,故椭圆方程为
,故椭圆方程为![]() .
.
(2)由(1)知![]() ,由
,由![]() 的平分线垂直
的平分线垂直![]() 知直线
知直线![]() 与
与![]() 关于
关于![]() 对称,
对称,
设![]() 的斜率为
的斜率为![]() ,则
,则![]() 的斜率为
的斜率为![]() ,
,![]() ,
,
与椭圆联立得![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以![]()
所以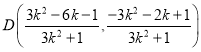 ,同理得
,同理得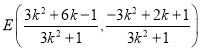 ,
,
所以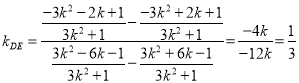 ,
,
由弦长公式得![]() ,解得
,解得![]() 或
或![]()
不妨设![]() 在
在![]() 的左侧,
的左侧,
当![]() 时,
时,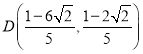 ,
,![]() ;
;
当![]() 时,
时,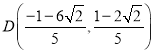 ,
,![]() .
.
综上所述,![]() 或
或![]() .
.

 考前必练系列答案
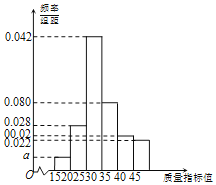
考前必练系列答案【题目】为保障食品安全,某地食品药监管部门对辖区内甲、乙两家食品企业进行检查,分别从这两家企业生产的某种同类产品中随机抽取了100件作为样本,并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下:
质量指标值 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45] |
等级 | 次品 | 二等品 | 一等品 | 二等品 | 三等品 | 次品 |
根据质量指标值的分组,统计得到了甲企业的样本频率分布直方图和乙企业的样本频数分布表(如下面表,其中a>0).
质量指标值 | 频数 |
[15,20) | 2 |
[20,25) | 18 |
[25,30) | 48 |
[30,35) | 14 |
[35,40) | 16 |
[40,45] | 2 |
合计 | 100 |
(Ⅰ)现从甲企业生产的产品中任取一件,试估计该件产品为次品的概率;
(Ⅱ)为守法经营、提高利润,乙企业开展次品生产原因调查活动.已知乙企业从样本里的次品中随机抽取了两件进行分析,求这两件次品中恰有一件指标值属于[40,45]的产品的概率;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两企业食品质量的优劣情况进行比较.