题目内容
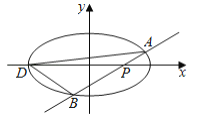
【题目】如图,椭圆![]()
![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() (
(![]() ,
,![]() )的动直线
)的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
⑴求椭圆![]() 的方程:
的方程:
⑵已知![]() 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线![]() 使得
使得![]() 的面积为
的面积为![]() ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)存在直线
;(2)存在直线![]() 方程
方程![]() 使得
使得![]() .
.
【解析】试题分析:(1)借助题设条件建立方程组求解;(2)依据题设运用直线与椭圆的位置关系进行探求.
试题解析:
(1)![]() 椭圆
椭圆![]() :
:![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,
两点,
当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() ,
,
![]() 点
点![]() 在椭圆
在椭圆![]() 上,
上,
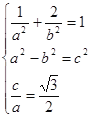 ,解得:
,解得:![]() ,………………4分
,………………4分
![]() 椭圆的方程为
椭圆的方程为![]() ………………………5分,
………………………5分,
(2)当直线![]() 与
与![]() 轴平行时,
轴平行时,![]() 不存在,…………………6分,
不存在,…………………6分,
![]() 设直线
设直线![]() 的方程为
的方程为![]() ,并设两点
,并设两点![]() ,
,![]() ,
,
联立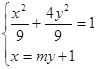 ,得
,得![]() ,
,
其判别式![]() ,…………8分,
,…………8分,
![]() ,
,![]() ,
,
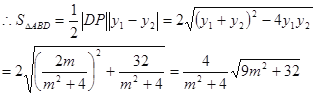 ,…………10分
,…………10分
假设存在直线![]() ,则有
,则有![]() ,
,
解得![]() ,负解删除,
,负解删除,![]() ,……………………12分
,……………………12分
故存在直线![]() 方程
方程![]() 使得
使得![]() …………13分.
…………13分.

练习册系列答案
相关题目