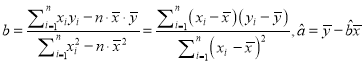题目内容
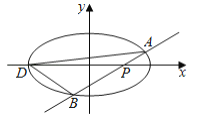
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
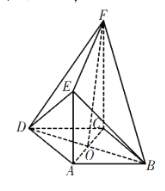
(1)求证:![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() 时,求
时,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)由菱形的性质可知![]() ,由
,由![]() 平面
平面![]() 可得
可得![]() ,由此可证
,由此可证![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,以
为原点,以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,以过点
轴,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的法向量及向量
的法向量及向量![]() ,由直线
,由直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,利用向量公式可求出
,利用向量公式可求出![]() 的长度.
的长度.
试题解析:(1)证明:![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() .………………(1分)
.………………(1分)
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,…………(2分)
,…………(2分)
![]() ,………………(3分)
,………………(3分)
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,………………(4分)
,………………(4分)
![]() 平面
平面![]() .………………(5分)
.………………(5分)
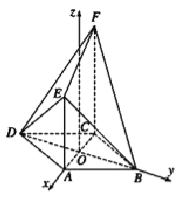
(2)以![]() 为原点,以
为原点,以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,以过点
轴,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴建立空间直角坐标系.………………(6分)
轴建立空间直角坐标系.………………(6分)
则![]() .设
.设![]() ,则
,则![]() ,
,
![]() ,………………(7分)
,………………(7分)
设平面![]() 的法向量为
的法向量为![]() ,则
,则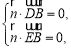 ………………(8分)
………………(8分)
即 令
令![]() ,得
,得![]() ,………………(9分)
,………………(9分)
 ,………………(10分)
,………………(10分)
![]() 直线
直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,
,
![]() ,………………(11分)
,………………(11分)
解得![]() 或
或![]() (舍),
(舍),![]() .………………(12分)
.………………(12分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款 | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() ,
,![]() 得到下表2:
得到下表2:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]()
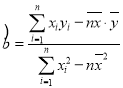
![]() )
)