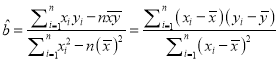题目内容
【题目】已知函数![]() (
(![]() )在
)在![]() 上的最小值为
上的最小值为![]() ,当把
,当把![]() 的图象上所有的点向右平移
的图象上所有的点向右平移![]() 个单位后,得到函数
个单位后,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)在△![]() 中,角
中,角![]() ,
,![]() ,
,![]() 对应的边分别是
对应的边分别是![]() ,
,![]() ,
,![]() ,若函数
,若函数![]() 在
在![]() 轴右侧的第一个零点恰为
轴右侧的第一个零点恰为![]() ,
,![]() ,求△
,求△![]() 的面积
的面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用三角函数在区间上的最值求得![]() 的值,然后根据图象平移求得函数
的值,然后根据图象平移求得函数![]() 的解析式;(2)由函数
的解析式;(2)由函数![]() 在
在![]() 轴右侧的第一个零点恰为
轴右侧的第一个零点恰为![]() ,得
,得![]() ,从而求得
,从而求得![]() 的值,利用余弦定理结合基本不等式求得
的值,利用余弦定理结合基本不等式求得![]() 的最大值,利用三角形面积公式求得△
的最大值,利用三角形面积公式求得△![]() 的面积
的面积![]() 的最大值.
的最大值.
试题解析:(1)∵函数![]() (
(![]() )在
)在![]() 上的最小值为
上的最小值为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
把![]() 的图象上所有的点向右平移
的图象上所有的点向右平移![]() 个单位后,得到的函数
个单位后,得到的函数![]()
![]() ,
,
∴函数![]() 的解析式为
的解析式为![]() .
.
(2)∵函数![]() 在
在![]() 轴右侧的第一个零点恰为
轴右侧的第一个零点恰为![]() ,
,
所以由![]() ,解得
,解得![]() ,
,![]() ,
,
可得,![]() ,
,![]() ,令
,令![]() ,可得
,可得![]() .
.
∵![]() ,
,
∴由余弦定理可得![]() ,
,
∴![]() ,
,
故△![]() 的面积
的面积![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】在高中学习过程中,同学们经常这样说:“如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
求数学成绩![]() 关于物理成绩
关于物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]()
若某位学生的物理成绩为80分,预测他的数学成绩;