题目内容
【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别交单位圆于A,B两点.已知A,B两点的横坐标分别是 ![]() ,
, ![]() .
. 
(1)求tan(α+β)的值;
(2)求α+2β的值.
【答案】
(1)解:由已知条件即三角函数的定义可知 ![]() ,
,
因为α为锐角,则sinα>0,从而 ![]()
同理可得 ![]() ,
,
因此 ![]() .
.
所以tan(α+β)= 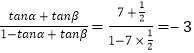
(2)解:tan(α+2β)=tan[(α+β)+β]= 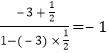 ,
,
又 ![]() ,故
,故 ![]() ,
,
所以由tan(α+2β)=﹣1得 ![]()
【解析】(1)先由已知条件得 ![]() ;再求sinα、sinβ进而求出tanα、tanβ;最后利用tan(α+β)=
;再求sinα、sinβ进而求出tanα、tanβ;最后利用tan(α+β)= ![]() 解之.(2)利用第一问把tan(α+2β)转化为tan[(α+β)+β]求之,再根据α+2β的范围确定角的值.
解之.(2)利用第一问把tan(α+2β)转化为tan[(α+β)+β]求之,再根据α+2β的范围确定角的值.

练习册系列答案
相关题目
【题目】我省城乡居民社会养老保险个人年缴费分100,200,300,400,500,600,700,800,900,1000(单位:元)十个档次,某社区随机抽取了50名村民,按缴费在100:500元,600:1000元,以及年龄在20:39岁,40:59岁之间进行了统计,相关数据如下:
100﹣500元 | 600﹣1000 | 总计 | |
20﹣39 | 10 | 6 | 16 |
40﹣59 | 15 | 19 | 34 |
总计 | 25 | 25 | 50 |
(1)用分层抽样的方法在缴费100:500元之间的村民中随机抽取5人,则年龄在20:39岁之间应抽取几人?
(2)在缴费100:500元之间抽取的5人中,随机选取2人进行到户走访,求这2人的年龄都在40:59岁之间的概率.