Question

【题目】f（x）=2cos2x﹣2acosx﹣1﹣2a的最小值为g（a），a∈R
（1）求g（a）；
（2）若g（a）= ，求a及此时f（x）的最大值．

Answer 1

【答案】
（1）解：f（x）=2cos2x﹣2acosx﹣1﹣2a=2（cosx﹣ ）2﹣ ﹣2a﹣1，

当﹣1≤ ≤1，g（a）=﹣ ﹣2a﹣1，

＞1时，时g（a）=1﹣4a

＜﹣1时，g（a）=1，

综合以上，g（a）=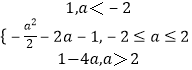

（2）解：令1﹣4a= 求得a= 不符合题意，

令﹣ ﹣2a﹣1= ，求得a=﹣1或﹣3（舍去）

故f（x）的最大值为5，a的值为﹣1

【解析】（1）利用二倍角公式对函数解析式化简，配方后，讨论 的范围确定g（a）的解析式，最后综合即可．（2）利用每个范围段的解析式求得a的值，最后验证a即可．