题目内容
【题目】定义:若数列![]() 满足所有的项均由
满足所有的项均由![]() 构成且其中
构成且其中![]() 有
有![]() 个,
个,![]() 有
有![]() 个
个![]() ,则称
,则称![]() 为“
为“![]() ﹣数列”.
﹣数列”.
(1)![]() 为“
为“![]() ﹣数列”
﹣数列”![]() 中的任意三项,则使得
中的任意三项,则使得![]() 的取法有多少种?
的取法有多少种?
(2)![]() 为“
为“![]() ﹣数列”
﹣数列”![]() 中的任意三项,则存在多少正整数
中的任意三项,则存在多少正整数![]() 对使得
对使得![]() 且
且![]() 的概率为
的概率为![]() .
.
【答案】(1)16;(2)115.
【解析】
(1)易得使得![]() 的情况只有“
的情况只有“![]() ”,“
”,“![]() ”两种,再根据组合的方法求解两种情况分别的情况数再求和即可.
”两种,再根据组合的方法求解两种情况分别的情况数再求和即可.
(2)易得“![]() ”共有
”共有![]() 种,“
种,“![]() ”共有
”共有![]() 种.再根据古典概型的方法可知
种.再根据古典概型的方法可知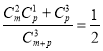 ,利用组合数的计算公式可得
,利用组合数的计算公式可得![]() ,当
,当![]() 时根据题意有
时根据题意有![]() ,共
,共![]() 个;
个;
当![]() 时求得
时求得![]() ,再根据
,再根据![]() 换元根据整除的方法求解满足的正整数对即可.
换元根据整除的方法求解满足的正整数对即可.
解:(1)三个数乘积为![]() 有两种情况:“
有两种情况:“![]() ”,“
”,“![]() ”,
”,
其中“![]() ”共有:
”共有:![]() 种,
种,
“![]() ”共有:
”共有:![]() 种,
种,
利用分类计数原理得:
![]() 为“
为“![]() ﹣数列”
﹣数列”![]() 中的任意三项,
中的任意三项,
则使得![]() 的取法有:
的取法有:![]() 种.
种.
(2)与(1)同理,“![]() ”共有
”共有![]() 种,
种,
“![]() ”共有
”共有![]() 种,
种,
而在“![]() ﹣数列”中任取三项共有
﹣数列”中任取三项共有![]() 种,
种,
根据古典概型有: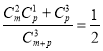 ,
,
再根据组合数的计算公式能得到:
![]() ,
,
![]() 时,应满足
时,应满足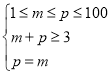 ,
,
![]() ,共
,共![]() 个,
个,
![]() 时,
时,
应满足 ,
,
视![]() 为常数,可解得
为常数,可解得![]() ,
,
![]()
![]() ,
,
根据![]() 可知,
可知,![]() ,
,
![]() ,
,
![]() ,
,
根据![]() 可知,
可知,![]() ,(否则
,(否则![]() ),
),
下设![]() ,
,
则由于![]() 为正整数知
为正整数知![]() 必为正整数,
必为正整数,
![]() ,
,
![]() ,
,
化简上式关系式可以知道:![]() ,
,
![]() 均为偶数,
均为偶数,
![]() 设
设![]() ,
,
则![]()
![]() ,
,
由于![]() 中必存在偶数,
中必存在偶数,
![]() 只需
只需![]() 中存在数为
中存在数为![]() 的倍数即可,
的倍数即可,
![]() ,
,
![]() .
.
检验:![]() 符合题意,
符合题意,
![]() 共有
共有![]() 个,
个,
综上所述:共有![]() 个数对
个数对![]() 符合题意.
符合题意.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目