题目内容
【题目】2019年国庆节假期期间，某商场为掌握假期期间顾客购买商品人次，统计了10月1日7：00﹣23：00这一时间段内顾客购买商品人次，统计发现这一时间段内顾客购买商品共5000人次顾客购买商品时刻的的频率分布直方图如下图所示，其中时间段7：0011：00，11：0015：00，15：00～19：00，19：00～23：00，依次记作[7，11），[11，15），[15，19），[19，23].
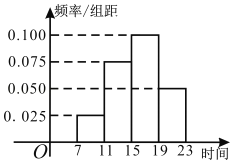
（1）求该天顾客购买商品时刻的中位数t与平均值
（同一组中的数据用该组区间的中点值代表）；
（2）由频率分布直方图可以近似认为国庆节假期期间该商场顾客购买商品时刻服从正态分布N（μ，δ2），其中μ近似为，δ＝3.6，估计2019年国庆节假期期间（10月1日﹣10月7日）该商场顾客在12：12﹣19：24之间购买商品的总人次（结果保留整数）；
（3）为活跃节日气氛，该商场根据题中的4个时间段分组，采用分层抽样的方法从这5000个样本中随机抽取10个样本（假设这10个样本为10个不同顾客）作为幸运客户，再从这10个幸运客户中随机抽取4人每人奖励500元购物券，其他幸运客户每人奖励200元购物券，记获得500元购物券的4人中在15：00﹣19：00之间购买商品的人数为X，求X的分布列与数学期望；
参考数据：若T～N（μ，σ2），则①P（μ﹣σ＜T≤μ+σ）＝0.6827；②P（μ﹣2σ＜T≤μ+2σ）＝0.9545；③P（μ﹣3σ＜T≤μ+3σ）＝0.9973.
【答案】（1）16,15.8；（2）23895；（3）分布列见解析，
【解析】
（1）中位数t∈（15，19），4×（0.025+0.075）+（t﹣15）×0.100＝0.5，再计算平均值得到答案.
（2）根据正态分布得到P（12.2＜T＜19.4）＝0.6827，计算得到答案.
（3）X可能取值为0，1，2，3，4，计算概率得到分布列，再计算数学期望得到答案.
（1）根据题意，中位数t∈（15，19），
由4×（0.025+0.075）+（t﹣15）×0.100＝0.5，得t＝16，
4（9×0.025+13×0.075+17×0.100+21×0.050）＝15.8；
（2）商场顾客购买商品时刻服从正态分布N（15.8，3.62），μ﹣δ＝12.2，μ+δ＝19.4，
所以2019年国庆节假期期间，商场顾客在12：12﹣19：24之间购买商品的概率为：
P（12.2＜T＜19.4）＝0.6827，所以人数为5000×0.6827×7≈23895；
（3）根据题意X可能取值为0，1，2，3，4，
P（X＝0）
，P（X＝1）
，
P（X＝2）
，P（X＝3）
，P（X＝4）
，
X的分布列如下
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
E（X）＝0
1
2
.
