题目内容
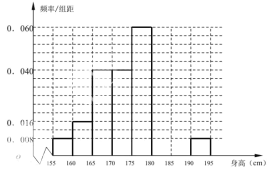
【题目】在某批次的某种灯泡中,随机地抽取![]() 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命(天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)根据频率分布表中的数据,写出![]() 、
、![]() 的值;
的值;
(2)某人从灯泡样品中随机地购买了![]() 个,如果这
个,如果这![]() 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求![]() 的最小值;
的最小值;
(3)某人从这个批次的灯泡中随机地购买了![]() 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用![]() 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)分布列见解析,
;(3)分布列见解析,![]() .
.
【解析】
(1)根据频数、频率和样本容量之间的关系可得出![]() 、
、![]() 的值;
的值;
(2)由频率分布表知按分层抽样法,购买灯泡数![]() 个,由此能求出
个,由此能求出![]() 的最小值;
的最小值;
(3)![]() 的所有取值为
的所有取值为![]() 、
、![]() 、
、![]() 、
、![]() ,分别求出相对应的概率,由此能求出
,分别求出相对应的概率,由此能求出![]() 的分布列和数学期望.
的分布列和数学期望.
(1)由题意可得![]() ,
,![]() ;
;
(2)由表可知:灯泡样品中优等品有![]() 个,正品有
个,正品有![]() 个,次品有
个,次品有![]() 个,
个,
![]() 优等品、正品和次品的比例为
优等品、正品和次品的比例为![]() ,
,
![]() 按分层抽样法,购买灯泡数为
按分层抽样法,购买灯泡数为![]() 个,
个,
因此,![]() 的最小值为
的最小值为![]() ;
;
(3)![]() 的所有取值为
的所有取值为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
由题意,购买一个灯泡,且这个灯泡是次品的概率为![]() ,
,
从本批次灯泡中购买![]() 个,可看成
个,可看成![]() 次独立重复试验,则
次独立重复试验,则![]() .
.
![]() ,
,![]() ,
,
![]() ,
, .
.
所以,随机变量![]() 的分布列如下表所示:
的分布列如下表所示:
|
|
|
|
|
|
|
|
|
|
因此,随机变量![]() 的数学期望为
的数学期望为![]() .
.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目