Question

【题目】已知函数f（x）=log3 ，g（x）=﹣2ax+a+1，h（x）=f（x）+g（x）．
（Ⅰ）当a=﹣1时，证明h（x）是奇函数；
（Ⅱ）若关于x的方程f（x）=log3g（x）有两个不等实数根，求实数a的取值范围．

Answer 1

【答案】解：（Ⅰ）证明：当a=﹣1时，
f（x）=log3 ，g（x）=2x，
h（x）=log3 +2x，
定义域为（﹣∞，﹣1）∪（1，+∞），
又∵h（﹣x）=log3 ﹣2x，
∴h（x）+h（﹣x）=log3 +log3 +2x﹣2x=0，
故h（x）为奇函数；
（Ⅱ）∵f（x）=log3g（x），
∴ =﹣2ax+a+1，且x∈（﹣∞，﹣1）∪（1，+∞），
∴（1﹣2x）a= ﹣1=﹣ ，
显然a≠0，
∴ =（x+1）（x﹣ ），
利用图象可知，当 ＞1时，
方程 =（x+1）（x﹣ ）在（﹣∞，﹣1）∪（1，+∞）内有两个不等实数根，
解得0＜a＜1．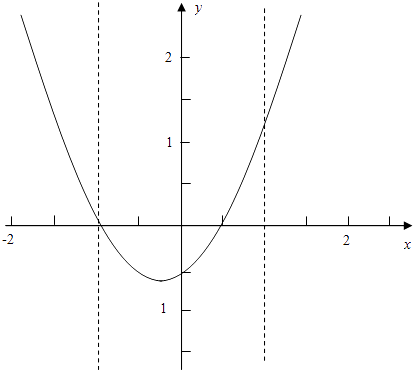

【解析】（Ⅰ）当a=﹣1时，化简h（x）=log3 +2x，并求其定义域为（﹣∞，﹣1）∪（1，+∞），再判断h（x）+h（﹣x）=0即可；（Ⅱ）化简可得 =﹣2ax+a+1，且x∈（﹣∞，﹣1）∪（1，+∞），从而可得 =（x+1）（x﹣ ），从而解得．
【考点精析】通过灵活运用函数的奇偶性和函数的零点，掌握偶函数的图象关于y轴对称；奇函数的图象关于原点对称；函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点即可以解答此题．