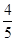题目内容
连掷两次骰子得到的点数分别为m和n,记向量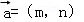 与向量
与向量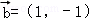 的夹角为θ,则
的夹角为θ,则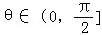 的概率是( )
的概率是( )
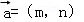 与向量
与向量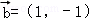 的夹角为θ,则
的夹角为θ,则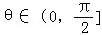 的概率是( )
的概率是( )A.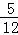 | B.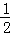 | C.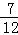 | D.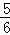 |
C
由题意知本题是一个古典概型,
试验发生包含的所有事件数6×6,
∵m>0,n>0,
∴ =(m,n)与
=(m,n)与 =(1,﹣1)不可能同向.
=(1,﹣1)不可能同向.
∴夹角θ≠0.
∵θ∈(0,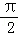 】
】
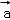 •
• ≥0,∴m﹣n≥0,
≥0,∴m﹣n≥0,
即m≥n.
当m=6时,n=6,5,4,3,2,1;
当m=5时,n=5,4,3,2,1;
当m=4时,n=4,3,2,1;
当m=3时,n=3,2,1;
当m=2时,n=2,1;
当m=1时,n=1.
∴满足条件的事件数6+5+4+3+2+1
∴概率P= =
=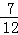 .
.
故选C.
试验发生包含的所有事件数6×6,
∵m>0,n>0,
∴
 =(m,n)与
=(m,n)与 =(1,﹣1)不可能同向.
=(1,﹣1)不可能同向.∴夹角θ≠0.
∵θ∈(0,
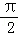 】
】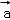 •
• ≥0,∴m﹣n≥0,
≥0,∴m﹣n≥0,即m≥n.
当m=6时,n=6,5,4,3,2,1;
当m=5时,n=5,4,3,2,1;
当m=4时,n=4,3,2,1;
当m=3时,n=3,2,1;
当m=2时,n=2,1;
当m=1时,n=1.
∴满足条件的事件数6+5+4+3+2+1
∴概率P=
 =
=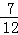 .
.故选C.

练习册系列答案
相关题目
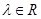 ,都有
,都有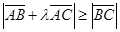 ,则
,则 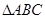 ( )
( )
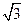
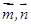 满足:对任意的
满足:对任意的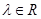 ,恒有
,恒有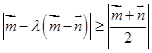 ,则( )
,则( )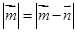
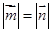
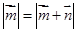
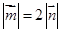
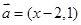 ,
,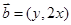 ,且
,且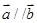 ,则y取最小值时,向量
,则y取最小值时,向量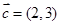 在
在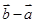 方向上的投影为( )
方向上的投影为( )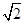
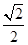
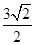
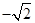
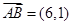 ,
,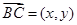 ,
,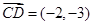 ,其中
,其中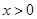
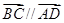 ,试求
,试求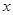 与
与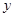 之间的表达式;
之间的表达式;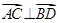 ,试求
,试求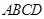 的面积。
的面积。 ·
· =-1,则|
=-1,则| |的最小值是( )
|的最小值是( )



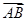 =λ
=λ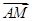 +μ
+μ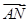 ,则λ+μ=( )
,则λ+μ=( )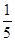 B.
B.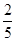 C.
C.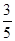 D.
D.