题目内容
【题目】已知函数y= 
+lg（﹣x2+4x﹣3）的定义域为M，
（1）求M；
（2）当x∈M时，求函数f（x）=a2x+2+34x（a＜﹣3）的最小值．
【答案】
（1）解：由题意，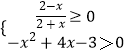 
，解得1≤x≤2，∴M=（1，2]
（2）解：令t=2x（t∈（2，4]），f（x）=g（t）=﹣4at+3t2=3（t+ 
）2﹣ 
1°﹣6＜a＜﹣3，即2＜﹣ ＜4时，g（t）min=g（﹣ ）=﹣ ；
2°a≤﹣6，即﹣ ≥4时，g（t）min=g（4）=48+16a
∴f（x）min=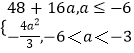 
【解析】（1）利用被开方数非负，真数大于0，建立不等式组，即可求得函数的定义域；（2）换元，利用配方法，结合函数的定义域，分类讨论，即可求得结论．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
