Question

【题目】设函数f（x）=x3+3x2+1，已知a≠0，且f（x）﹣f（a）=（x﹣b）（x﹣a）2 ， x∈R，则实数a= ， b= ．

Answer 1

【答案】-2；1
【解析】解：∵f（x）=x3+3x2+1，
∴f（x）﹣f（a）=x3+3x2+1﹣（a3+3a2+1）
=x3+3x2﹣（a3+3a2）
∵（x﹣b）（x﹣a）2=（x﹣b）（x2﹣2ax+a2）=x3﹣（2a+b）x2+（a2+2ab）x﹣a2b，
且f（x）﹣f（a）=（x﹣b）（x﹣a）2 ，
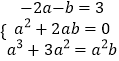∴ ，解得 或 （舍去），
故答案为：﹣2；1．
根据函数解析式化简f（x）﹣f（a），再化简（x﹣b）（x﹣a）2 ， 根据等式两边对应项的系数相等列出方程组，求出a、b的值．