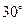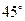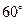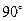题目内容
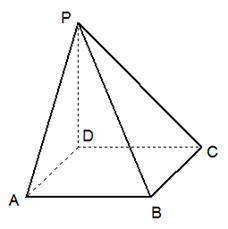
(本小题满分14分)如图,四棱锥P-ABCD是底面边长为1的正方形,PD⊥BC,PD=1,PC=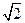 .
.
(Ⅰ)求证:PD⊥面ABCD;
(Ⅱ)求二面角A-PB-D的大小.
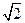 .
.(Ⅰ)求证:PD⊥面ABCD;
(Ⅱ)求二面角A-PB-D的大小.

(Ⅰ)略
(Ⅱ)二面角A-PB-D的大小为60°。
(Ⅱ)二面角A-PB-D的大小为60°。
(Ⅰ)证明: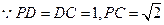 ,
,
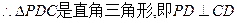 .……2分
.……2分
 又
又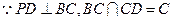 ,……4分
,……4分
∴ PD⊥面ABCD………6分
(Ⅱ)解:连结BD,设BD交AC于点O,
过O作OE⊥PB于点E,连结AE,
∵PD⊥面ABCD, ∴ ,
,
又∵AO⊥BD,∴AO⊥面PDB.
∴AO⊥PB,
∵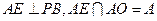 ,
,
∴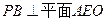 ,从而
,从而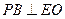 ,
,
故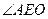 就是二面角A-PB-D的平面角.……………………10分
就是二面角A-PB-D的平面角.……………………10分
∵PD⊥面ABCD, ∴PD⊥BD,
∴在Rt△PDB中,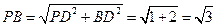 ,
,
又∵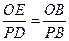 , ∴
, ∴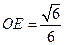 ,………………12分
,………………12分
 ∴
∴  .
.
故二面角A-PB-D的大小为60°.…………………14分
(也可用向量解)
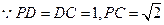 ,
,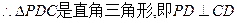 .……2分
.……2分 又
又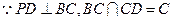 ,……4分
,……4分∴ PD⊥面ABCD………6分
(Ⅱ)解:连结BD,设BD交AC于点O,
过O作OE⊥PB于点E,连结AE,
∵PD⊥面ABCD, ∴
 ,
,又∵AO⊥BD,∴AO⊥面PDB.
∴AO⊥PB,
∵
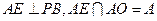 ,
,∴
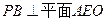 ,从而
,从而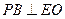 ,
,故
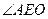 就是二面角A-PB-D的平面角.……………………10分
就是二面角A-PB-D的平面角.……………………10分∵PD⊥面ABCD, ∴PD⊥BD,
∴在Rt△PDB中,
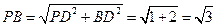 ,
,又∵
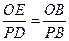 , ∴
, ∴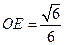 ,………………12分
,………………12分 ∴
∴  .
.故二面角A-PB-D的大小为60°.…………………14分
(也可用向量解)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

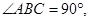
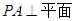 ,
,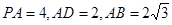 ,BC=6.
,BC=6.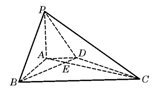
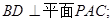
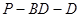 的大小.
的大小.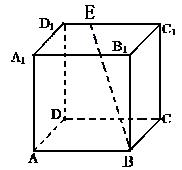
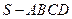 的底面是边长为
的底面是边长为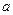 的正方形,且
的正方形,且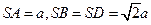 。
。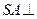 平面
平面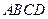 ;
;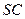 为四棱锥中最长的侧棱,点
为四棱锥中最长的侧棱,点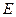 为
为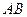 的中点.求直线SE.与平面SAC所成角的正弦值。
的中点.求直线SE.与平面SAC所成角的正弦值。
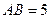 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.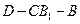 的平面角的正切值.
的平面角的正切值.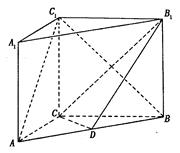
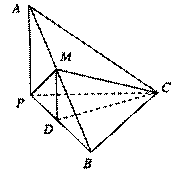
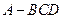 中,
中,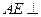 平面
平面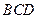 ,
,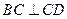 ,
,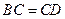 ,
,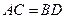 ,
,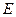 是
是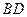 的中点;
的中点;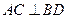 ;
;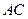 与平面
与平面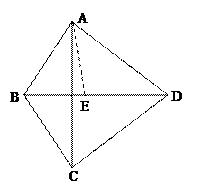
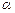 ,直线
,直线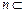 平面
平面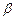 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )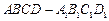 中,
中,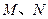 分别为
分别为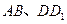 的中点,则异面直线
的中点,则异面直线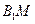 与
与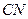 所成角是 ( )
所成角是 ( )