题目内容
3.若O是△ABC的外心,且$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{CO}$=$\overrightarrow{0}$,则角C=$\frac{2π}{3}$.分析 由$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{CO}$=$\overrightarrow{0}$,O是三角形外心,结合已知可判断三角形的形状.
解答 解:画出草图,如图示: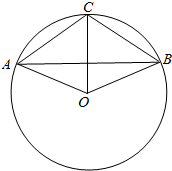 ,
,
∵$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{CO}$=$\overrightarrow{0}$,
由向量加法的运算,0是外心,
得:△AOC≌△BOC是等边三角形,
∴∠ACB=$\frac{2π}{3}$,
故答案为:$\frac{2π}{3}$.
点评 本题主要考查了向量的加法运算在三角形的形状判断中的应用,考查了三角形“心”(内心,外心,中心,垂心)的性质,属于基础试题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
11.字母N、Z、Q和R分别表示自然数集、整数集、有理数集和实数集,则它们之间的关系是( )
| A. | N?Q?Z?R | B. | N?Z?Q?R | C. | R?Q?Z?N | D. | Z?N?Q?R |
14.若α,β满足0<α,β<π,则α-2β的取值范围是( )
| A. | (-π,0) | B. | (-2π,π) | C. | (-π,2π) | D. | (0,2π) |
13.已知向量$\overrightarrow{a}$=(m+3,m-cos2α),$\overrightarrow{b}$=(n,$\frac{n}{2}$+sinα),其中m,n,α为实数,若$\overrightarrow{a}$=2$\overrightarrow{b}$,则$\frac{m}{n}$的取值范围是( )
| A. | [-1,$\frac{7}{5}$] | B. | [0,$\frac{7}{4}$] | C. | [-2,$\frac{7}{3}$] | D. | [-2,$\frac{7}{5}$] |