题目内容
11.设f(x)=$\frac{1}{2}$x2-tx+3lnx,g(x)=$\frac{2x+t}{{x}^{2}-3}$,且a,b为函数f(x)的极值点(0<a<b).(1)判断函数g(x)在区间[-b,-a]上的单调性,并证明你的结论;
(2)若曲线g(x)在x=1处的切线的斜率为-4,且方程g(x)-m=0(x≤0)有两个不等的实根,求实数m的取值范围.
分析 (1)利用导数的正负判断函数的单调性;
(2)先利用导数的几何意义求出t,进而得出单调区间,根据极值点和单调性模拟函数图象,利用数学结合解决问题.
解答 解:(1)f′(x)=x-t+$\frac{3}{x}$=$\frac{{x}^{2}-tx+3}{x}$
x=a,x=b为函数f(x)的极值点,
∴a,b是方程x2-tx+3=0的两根
∴a+b=t,ab=3.
g′(x)=-$\frac{2({x}^{2}+tx+3)}{({x}^{2}-3)^{2}}$=-$\frac{2(x+a)(x+b)}{({x}^{2}-3)^{2}}$. x≠$±\sqrt{3}$
∵0<a<b,ab=3,∴0<a<$\sqrt{3}$<b
∴-b<-$\sqrt{3}$<-a<0
当x∈(-b,-$\sqrt{3}$)和(-$\sqrt{3}$,-a)时,g′(x)>0,g(x)递增.
(2)g′(x)=-$\frac{2({x}^{2}+tx+3)}{({x}^{2}-3)^{2}}$
g′(1)=-4,解得t=4.
∴g(x)=$\frac{2x+4}{{x}^{2}-3}$
令g′(x)=-$\frac{2(x+1)(x+3)}{{(x}^{2}-3)^{2}}$=0
解得x=-3或-1.
当x∈(-∞,0]时,
当x=-3时,g(x)取得极小值-$\frac{1}{3}$
当x=-1时,g(x)取得极大值-1.
根据函数单调性,模拟函数图象如图:由图象可知: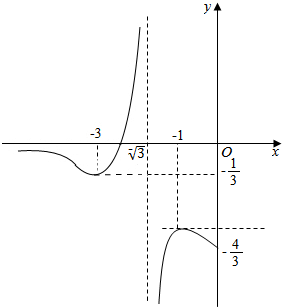
当-$\frac{1}{3}$<m<0或-$\frac{4}{3}$<m<-1时,方程g(x)-m=0有两个不相等的负实根.
点评 熟练掌握利用导数研究函数的单调性、极值和图象是解题的关键

练习册系列答案
相关题目