题目内容
(本小题满分10分)选修4-4:坐标系与参数方程.
已知点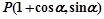 ,参数
,参数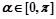 ,点Q在曲线C:
,点Q在曲线C: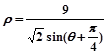 上.
上.
(1)求点P的轨迹方程和曲线C的直角坐标方程;
(2)求点P与点Q之间距离的最小值.
已知点
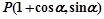 ,参数
,参数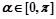 ,点Q在曲线C:
,点Q在曲线C: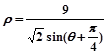 上.
上.(1)求点P的轨迹方程和曲线C的直角坐标方程;
(2)求点P与点Q之间距离的最小值.
(1) x+y=9.(2)|PQ|min=4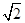 -1.
-1.
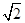 -1.
-1. 本试题主要是考查了参数方程的运用,以及直角坐标方程的求解和两点距离的最值问题
(1)因为由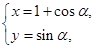 得点P的轨迹方程 (x-1)2+y2=1(y≥0), 又由又由
得点P的轨迹方程 (x-1)2+y2=1(y≥0), 又由又由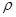 =
=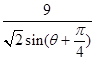 ,可得极坐标方程。
,可得极坐标方程。
(2)因为半圆(x-1)2+y2=1(y≥0)的圆心(1,0)到直线x+y=9的距离为4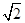 ,因此两点距离的最小值为点到直线的距离减去圆的半径。
,因此两点距离的最小值为点到直线的距离减去圆的半径。
解(1)由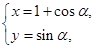 得点P的轨迹方程 (x-1)2+y2=1(y≥0),
得点P的轨迹方程 (x-1)2+y2=1(y≥0),
又由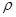 =
=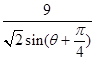 ,得
,得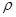 =
=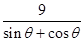 , ∴
, ∴ 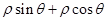 =9.
=9.
∴曲线C的直角坐标方程为 x+y=9.
(2)半圆(x-1)2+y2=1(y≥0)的圆心(1,0)到直线x+y=9的距离为4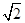 ,所以|PQ|min=4
,所以|PQ|min=4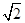 -1.
-1.
(1)因为由
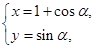 得点P的轨迹方程 (x-1)2+y2=1(y≥0), 又由又由
得点P的轨迹方程 (x-1)2+y2=1(y≥0), 又由又由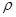 =
=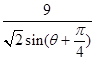 ,可得极坐标方程。
,可得极坐标方程。(2)因为半圆(x-1)2+y2=1(y≥0)的圆心(1,0)到直线x+y=9的距离为4
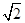 ,因此两点距离的最小值为点到直线的距离减去圆的半径。
,因此两点距离的最小值为点到直线的距离减去圆的半径。解(1)由
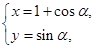 得点P的轨迹方程 (x-1)2+y2=1(y≥0),
得点P的轨迹方程 (x-1)2+y2=1(y≥0), 又由
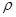 =
=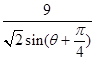 ,得
,得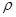 =
=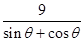 , ∴
, ∴ 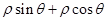 =9.
=9.∴曲线C的直角坐标方程为 x+y=9.
(2)半圆(x-1)2+y2=1(y≥0)的圆心(1,0)到直线x+y=9的距离为4
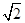 ,所以|PQ|min=4
,所以|PQ|min=4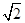 -1.
-1. 
练习册系列答案
相关题目
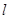 的参数方程为
的参数方程为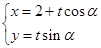 ,(
,(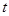 为参数,
为参数,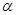 为倾斜角,且
为倾斜角,且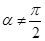 )与曲线
)与曲线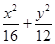 =1交于
=1交于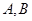 两点.
两点.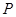 的坐标;
的坐标;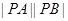 的最大值。
的最大值。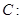
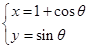 (
(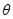 为参数)和直线
为参数)和直线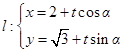 (其中为参数,
(其中为参数, 为直线的倾斜角),如果直线与圆
为直线的倾斜角),如果直线与圆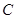 有公共点,求
有公共点,求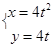 (t为参数)上,则
(t为参数)上,则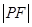 =( )
=( )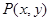 是圆
是圆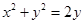 上的动点,
上的动点,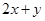 的取值范围;
的取值范围;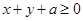 恒成立,求实数
恒成立,求实数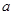 的取值范围。
的取值范围。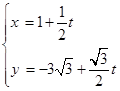 (t为参数)和圆
(t为参数)和圆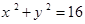 交于A、B两点,则AB的中点坐标为( )
交于A、B两点,则AB的中点坐标为( )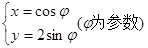 ,点M在椭圆上,点O为原点,则当
,点M在椭圆上,点O为原点,则当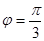 时,OM的斜率为( )
时,OM的斜率为( )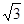
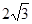
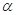 的终边与单位圆交于点
的终边与单位圆交于点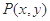 ,则( )
,则( )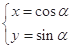
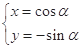
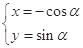
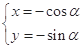
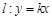 与曲线
与曲线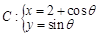 (参数
(参数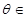 R)有唯一的公共点,则实数
R)有唯一的公共点,则实数 。
。