题目内容
7．函数f（x）=（a-1）x2+2ax+3为偶函数，那么f（x）在（-5，-2）上是增函数．分析 根据函数f（x）=（a-1）x2+2ax+3为偶函数，可得a=0，分析函数的图象和性质，可得答案．
解答 解：∵函数f（x）=（a-1）x2+2ax+3为偶函数，
∴f（-x）=（a-1）x2-2ax+3=f（x）=（a-1）x2+2ax+3，
∴a=0，
∴f（x）=-x2+3，
则函数的图象是开口朝下，且以y轴为对称轴的抛物线，
∴f（x）在（-5，-2）上是增函数，
故答案为：增函数．
点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
相关题目
15．函数f（x）=（x-1）ex-x2的单调递减区间为（ ）
| A． | （-∞，-ln2）、（0，+∞） | B． | （0，ln2） | C． | （-∞，ln2） | D． | （-∞，0）、（ln2，+∞） |
2．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x+1\\;x≥0}\\{3x+2\\;x＜0}\end{array}\right.$若互不相等的实数x1，x2，x3满足f（x1）=f（x2）=f（x3），则x1+x2+x3的取值范围是（ ）
| A． | [$\frac{7}{3}$，+∞） | B． | [$\frac{7}{3}$，4） | C． | （$\frac{7}{3}$，$\frac{11}{3}$] | D． | （$\frac{11}{3}$，+∞） |
12．
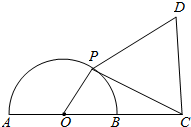如图，已知半圆的直径AB=2，点C在AB的延长线上，BC=1，点P为半圆上一个动点，以DC为边作等边三角形PCD，且点D与圆心分别在PC的两侧，则四边形OPDC面积的最大值为（ ）
如图，已知半圆的直径AB=2，点C在AB的延长线上，BC=1，点P为半圆上一个动点，以DC为边作等边三角形PCD，且点D与圆心分别在PC的两侧，则四边形OPDC面积的最大值为（ ）| A． | 2 | B． | $\frac{5\sqrt{3}}{4}$-2 | C． | $\frac{5\sqrt{3}}{4}$ | D． | 2+$\frac{5\sqrt{3}}{4}$ |