题目内容
2．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x+1\\;x≥0}\\{3x+2\\;x＜0}\end{array}\right.$若互不相等的实数x1，x2，x3满足f（x1）=f（x2）=f（x3），则x1+x2+x3的取值范围是（ ）| A． | [$\frac{7}{3}$，+∞） | B． | [$\frac{7}{3}$，4） | C． | （$\frac{7}{3}$，$\frac{11}{3}$] | D． | （$\frac{11}{3}$，+∞） |
分析 先画出函数的图象，得到x2+x3的值，求出x1的取值范围，从而得到答案．
解答 解：画出函数f（x）的图象，如图示：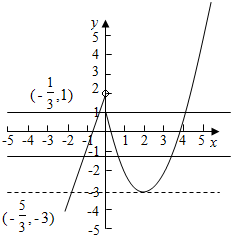
，
不妨设则x1＜x2＜x3，
则x2，x3关于直线x=2对称，
$-\frac{5}{3}$＜x1≤-$\frac{1}{3}$，
∴x2+x3=4，
∴$\frac{7}{3}$＜x1+x2+x3≤$\frac{11}{3}$，
即x1+x2+x3的取值范围是（$\frac{7}{3}$，$\frac{11}{3}$]，
故选：C．
点评 本题考查了分段函数的应用问题，考查了函数的对称性，是一道中档题
练习册系列答案
期末集结号系列答案
相关题目