题目内容
20.在△ABC中,已知∠A=60°,∠B=45°,那么a:b的值为( )| A. | 1:$\sqrt{2}$ | B. | $\sqrt{2}:1$ | C. | $\sqrt{2}:\sqrt{3}$ | D. | $\sqrt{3}:\sqrt{2}$ |
分析 根据正弦定理进行计算即可.
解答 解:∵∠A=60°,∠B=45°,
∴a:b=sinA:sinB=sin60°:sin45°=$\frac{\sqrt{3}}{2}:$$\frac{\sqrt{2}}{2}$=$\sqrt{3}:\sqrt{2}$,
故选:D
点评 本题主要考查正弦定理的应用,比较基础.

练习册系列答案
相关题目
16.函数f(x)=$\frac{\sqrt{10+9x-{x}^{2}}}{lg(x-1)}$的定义域为( )
| A. | [1,10] | B. | [1,2)∪(2,10] | C. | (1,10] | D. | (1,2)∪(2,10] |
12.如图C是△PAB边AB内的一点,下列说法正确的是( )
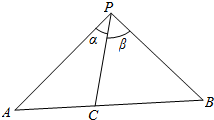

| A. | PCsin(α+β)=PBsinα+PAsinβ | B. | PCsin(α+β)=PAsinα+PBsinβ | ||
| C. | $\frac{sin(α+β)}{PC}$=$\frac{sinα}{PB}$+$\frac{sinβ}{PA}$ | D. | $\frac{sin(α+β)}{PC}$=$\frac{sinα}{PA}$+$\frac{sinβ}{PB}$ |