题目内容
三棱柱ABC—A1B1C1中,侧棱与底面垂直,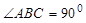 ,
, 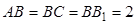 ,
,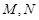 分别是
分别是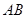 ,
,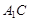 的中点.
的中点.
(1)求直线MN与平面A1B1C所成的角;
 (2)在线段AC上是否存在一点E,使得二面角E-B1A1-C的余弦值 为
(2)在线段AC上是否存在一点E,使得二面角E-B1A1-C的余弦值 为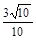 ?若存在,求出AE的长,若不存在,请说明理由.
?若存在,求出AE的长,若不存在,请说明理由.
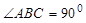 ,
, 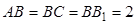 ,
,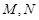 分别是
分别是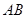 ,
,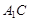 的中点.
的中点. (1)求直线MN与平面A1B1C所成的角;
 (2)在线段AC上是否存在一点E,使得二面角E-B1A1-C的余弦值 为
(2)在线段AC上是否存在一点E,使得二面角E-B1A1-C的余弦值 为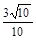 ?若存在,求出AE的长,若不存在,请说明理由.
?若存在,求出AE的长,若不存在,请说明理由.(1)900;(2)存在,AE=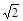
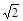
(1)本题适合利用空间向量求解.要知道线面角的向量求法.
(2)利用向量的方法在线段AC上的一点E,就要用到向量共线的条件,表示出E的坐标,然后根据二面角的余弦值,确定E坐标中的参数的值,进而可求出AE的长.
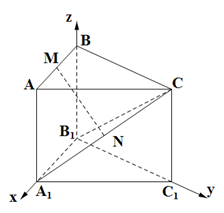
解:(1)如图,以B1为原点建立空间直角坐标系 B1-XYZ
B1-XYZ
则B1(0,0,0),C(0,2,2),A1(2,0,0),B(0,0,2),则M(1,0,2), A(2,0,2),(0,2,2) ,N(1,1,1)------------2分
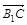 =(0,2,2),
=(0,2,2),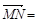 (0,1,-1),
(0,1,-1),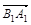 =(2,0,0)
=(2,0,0)
因为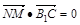 ,且
,且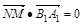 ,--------4分
,--------4分
所以MN⊥平面A1B1C
即MN与平面A1B1C所成的角为900 ------------------5分
(2)设E(x,y,z),且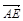 =
=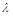
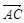 , --------------6分
, --------------6分
则(x-2,y,z-2)=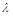 (-2,2,0)
(-2,2,0)
解得x=2-2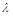 ,y=2
,y=2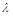 ,z=2,
,z=2,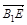 =(2-2
=(2-2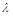 ,2
,2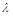 ,2) ---------7分
,2) ---------7分
由(1)可知平面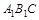 的法向量为
的法向量为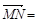 (0,1,-1),设平面
(0,1,-1),设平面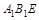 的法向量为
的法向量为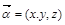 ,
,
则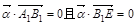 ,
,
则可解得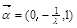 , ----------------9分
, ----------------9分
于是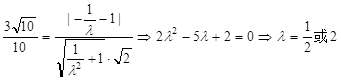 -------11分
-------11分
由于点E在线段上,所以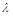 =
=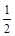 ,此时AE=
,此时AE=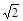 ----------12分
----------12分
(2)利用向量的方法在线段AC上的一点E,就要用到向量共线的条件,表示出E的坐标,然后根据二面角的余弦值,确定E坐标中的参数的值,进而可求出AE的长.
解:(1)如图,以B1为原点建立空间直角坐标系
 B1-XYZ
B1-XYZ
则B1(0,0,0),C(0,2,2),A1(2,0,0),B(0,0,2),则M(1,0,2), A(2,0,2),(0,2,2) ,N(1,1,1)------------2分
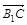 =(0,2,2),
=(0,2,2),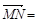 (0,1,-1),
(0,1,-1),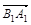 =(2,0,0)
=(2,0,0)因为
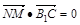 ,且
,且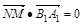 ,--------4分
,--------4分所以MN⊥平面A1B1C
即MN与平面A1B1C所成的角为900 ------------------5分
(2)设E(x,y,z),且
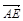 =
=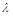
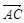 , --------------6分
, --------------6分则(x-2,y,z-2)=
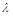 (-2,2,0)
(-2,2,0)解得x=2-2
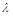 ,y=2
,y=2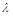 ,z=2,
,z=2,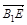 =(2-2
=(2-2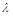 ,2
,2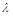 ,2) ---------7分
,2) ---------7分由(1)可知平面
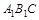 的法向量为
的法向量为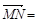 (0,1,-1),设平面
(0,1,-1),设平面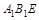 的法向量为
的法向量为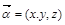 ,
,则
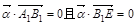 ,
,则可解得
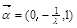 , ----------------9分
, ----------------9分 于是
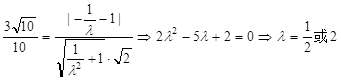 -------11分
-------11分由于点E在线段上,所以
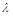 =
=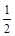 ,此时AE=
,此时AE=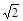 ----------12分
----------12分
练习册系列答案
相关题目

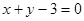 ,则
,则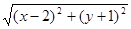 的最小值等于.
的最小值等于.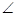 BAC=
BAC=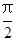 ,|AB|=|AC|=|CC1|=1.已知G、E分别为A1 B1和CC1的中点,D与F分别为线段AC和AB上的动点(不含端点),若GD⊥EF,则线段DF的长度的取值范围是
,|AB|=|AC|=|CC1|=1.已知G、E分别为A1 B1和CC1的中点,D与F分别为线段AC和AB上的动点(不含端点),若GD⊥EF,则线段DF的长度的取值范围是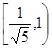 .
.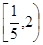
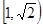
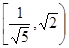
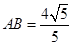 ,一块直角三角板
,一块直角三角板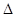 PBD的边
PBD的边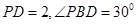 ,且
,且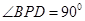 ,如图.
,如图.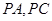 的长;
的长;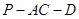 的平面角的余弦值.
的平面角的余弦值.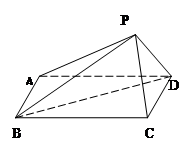
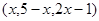 ,B
,B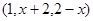 ,当
,当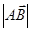 取最小值时,
取最小值时,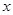 的值等于_________
的值等于_________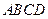 中,
中, 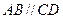 ,
,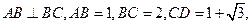 过
过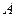 作
作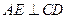 ,垂足为
,垂足为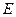 ,
,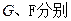
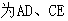 的中点,现将
的中点,现将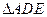 沿
沿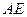 折叠,使得
折叠,使得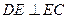 .
.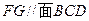 ;
;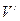 ,求V
,求V
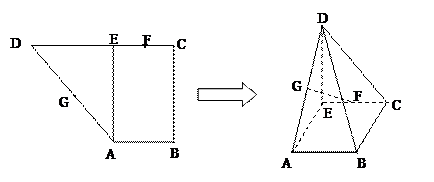

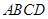 中,
中,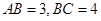 ,将
,将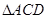 沿着
沿着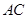 折成
折成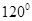 的二面角,则
的二面角,则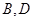 两点的距离为
两点的距离为