题目内容
在直三棱柱A1 B1 C1—ABC中,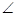 BAC=
BAC=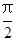 ,|AB|=|AC|=|CC1|=1.已知G、E分别为A1 B1和CC1的中点,D与F分别为线段AC和AB上的动点(不含端点),若GD⊥EF,则线段DF的长度的取值范围是
,|AB|=|AC|=|CC1|=1.已知G、E分别为A1 B1和CC1的中点,D与F分别为线段AC和AB上的动点(不含端点),若GD⊥EF,则线段DF的长度的取值范围是
 BAC=
BAC=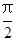 ,|AB|=|AC|=|CC1|=1.已知G、E分别为A1 B1和CC1的中点,D与F分别为线段AC和AB上的动点(不含端点),若GD⊥EF,则线段DF的长度的取值范围是
,|AB|=|AC|=|CC1|=1.已知G、E分别为A1 B1和CC1的中点,D与F分别为线段AC和AB上的动点(不含端点),若GD⊥EF,则线段DF的长度的取值范围是A.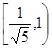 . . | B.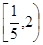 | C.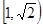 | D.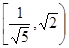 |
A
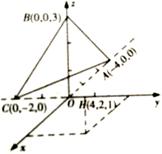
根据直三棱柱中三条棱两两垂直,本题考虑利用空间坐标系解决.建立如图所示的空间直角坐标系,设出F、D的坐标,求出向量 DG , EF ,利用GD⊥EF求得关系式,写出DF的表达式,然后利用二次函数求最值即可.
解:建立如图所示的空间直角坐标系,
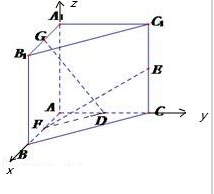
则A(0,0,0),E(0,1,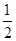 ),
),
G(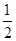 ,0,1),F(x,0,0),D(0,y,0)由于
,0,1),F(x,0,0),D(0,y,0)由于
GD⊥EF,所以 x+2y-1=0
DF2= x2+y2 = 5y2-4y+1 = 5(y- )2+
)2+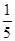 ,
,
当y= 时,线段DF长度的最小值是
时,线段DF长度的最小值是 ,
,
当y=1时,线段DF长度的最大值是 1
而不包括端点,故y=1不能取;
故答案为:[ ,1).可知结论选A
,1).可知结论选A
解:建立如图所示的空间直角坐标系,

则A(0,0,0),E(0,1,
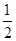 ),
),G(
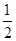 ,0,1),F(x,0,0),D(0,y,0)由于
,0,1),F(x,0,0),D(0,y,0)由于GD⊥EF,所以 x+2y-1=0
DF2= x2+y2 = 5y2-4y+1 = 5(y-
 )2+
)2+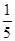 ,
,当y=
 时,线段DF长度的最小值是
时,线段DF长度的最小值是 ,
,当y=1时,线段DF长度的最大值是 1
而不包括端点,故y=1不能取;
故答案为:[
 ,1).可知结论选A
,1).可知结论选A
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的切线,则此切线段的长度为_______.
的切线,则此切线段的长度为_______.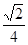 的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为( )
的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为( )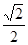 C.1 D.
C.1 D.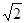
 求
求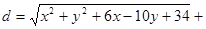
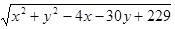 的最小值.
的最小值.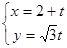 (
(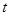 为参数)被曲线
为参数)被曲线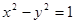 截得的弦长为( )
截得的弦长为( )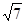
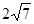
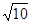
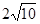
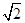
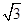
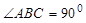 ,
, 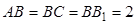 ,
,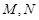 分别是
分别是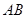 ,
,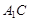 的中点.
的中点. 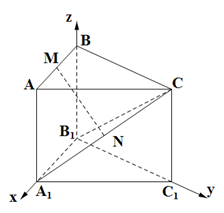 (2)在线段AC上是否存在一点E,使得二面角E-B1A1-C的余弦值 为
(2)在线段AC上是否存在一点E,使得二面角E-B1A1-C的余弦值 为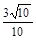 ?若存在,求出AE的长,若不存在,请说明理由.
?若存在,求出AE的长,若不存在,请说明理由.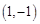 到直线
到直线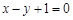 的距离是 ( ▲ )
的距离是 ( ▲ )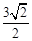
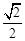
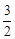
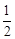
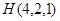 到平面
到平面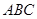 的距离是 .
的距离是 .