题目内容
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1.D是棱CC1上的中点,P是AD的延长线与A1C1的延长线的交点.
(1)求二面角A-A1D-B的平面角的余弦值;
(2)求点C到平面B1DP的距离.
(1)求二面角A-A1D-B的平面角的余弦值;
(2)求点C到平面B1DP的距离.

(1) ;(2)见解析.
;(2)见解析.
 ;(2)见解析.
;(2)见解析.本试题主要考查了立体几何中二面角的求解和点到面的距离的综合运用。
解:如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1).D(0,1, )
)

设平面BA1D的一个法向量为n1=(x,y,z),
 解得
解得
取 ,得n1=(2,-1,2).
,得n1=(2,-1,2).
又n2=(1,0,0)为平面AA1D的一个法向量,
∴cos〈n1·n2〉= =
= =
= .
.
故二面角A-A1D-B的平面角的余弦值为 .
.
(3)∵ =(1,-2,0),
=(1,-2,0), =
= ,
,
设平面B1DP的一个法向量为n3=(a1,b1,c1).

令c1=1,可得n3= .
.
又 =
= ,
,
∴C到平面B1DP的距离d= =
= .
.
解:如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1).D(0,1,
 )
)
设平面BA1D的一个法向量为n1=(x,y,z),
 解得
解得
取
 ,得n1=(2,-1,2).
,得n1=(2,-1,2).又n2=(1,0,0)为平面AA1D的一个法向量,
∴cos〈n1·n2〉=
 =
= =
= .
.故二面角A-A1D-B的平面角的余弦值为
 .
.(3)∵
 =(1,-2,0),
=(1,-2,0), =
= ,
,设平面B1DP的一个法向量为n3=(a1,b1,c1).

令c1=1,可得n3=
 .
.又
 =
= ,
,∴C到平面B1DP的距离d=
 =
= .
.
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
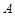 、
、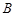 、
、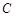 ,若
,若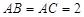 ,
,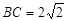 ,球心到平面
,球心到平面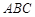 的距离为1,则球的表面积为( )
的距离为1,则球的表面积为( )
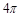
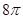

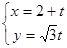 (
(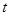 为参数)被曲线
为参数)被曲线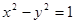 截得的弦长为( )
截得的弦长为( )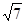
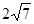
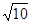
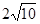
 中,M、N分别为AB,AC上的点,满足
中,M、N分别为AB,AC上的点,满足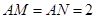 ,沿MN将
,沿MN将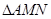 折起,使得平面AMN与平面MNCB所成的二面角为
折起,使得平面AMN与平面MNCB所成的二面角为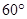 ,则A点到平面MNCB的距离为
,则A点到平面MNCB的距离为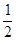
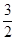
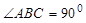 ,
, 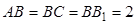 ,
,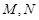 分别是
分别是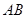 ,
,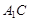 的中点.
的中点. 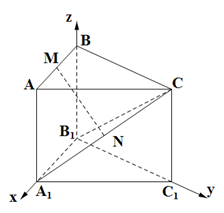 (2)在线段AC上是否存在一点E,使得二面角E-B1A1-C的余弦值 为
(2)在线段AC上是否存在一点E,使得二面角E-B1A1-C的余弦值 为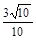 ?若存在,求出AE的长,若不存在,请说明理由.
?若存在,求出AE的长,若不存在,请说明理由.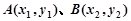 分别在直线
分别在直线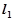 :
: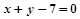 和
和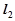 :
: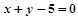 上移动,则
上移动,则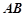 中点
中点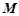 到原点距离的最小值为 ( )
到原点距离的最小值为 ( )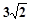
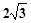
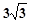
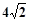
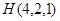 到平面
到平面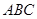 的距离是 .
的距离是 .
 ︱PQ︱=" " 。
︱PQ︱=" " 。