题目内容
9.设数列{an}是以1为首项,2为公差的等差数列,数列{bn}是以1为首项,2为公比的等比数列,则a${\;}_{{b}_{1}}$+a${\;}_{{b}_{2}}$+…+a${\;}_{{b}_{10}}$=2036.分析 利用等差数列和等比数列的通项公式即可得出an,bn.再利用等比数列的前n项和公式即可得出.
解答 解:∵数列{an}是以1为首项,2为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,
∴an=1+2(n-1)=2n-1,${b}_{n}={2}^{n-1}$.
∴${a}_{{b}_{n}}$=2bn-1=2•2n-1-1=2n-1.
∴${a_{b_1}}+{a_{b_2}}+…+{a_{{b_{10}}}}$=(2-1)+(22-1)+…+(210-1)=$\frac{2(1-{2}^{10})}{1-2}$-10=211-12=2048-12=2036
故答案为:2036
点评 本题考查了等比数列和等差数列的通项公式及其前n项和公式的计算,考查学生的计算能力.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
1.已知|$\overrightarrow{a}$|=2,$\overrightarrow{b}$为单位向量,$\overrightarrow{a}•\overrightarrow{b}$=1,则向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
18. 下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
(注:标准差s=$\sqrt{\frac{1}{n}[{{({x_1}-\overline x)}^2}+{{({x_2}-\overline x)}^2}+…+{{({x_n}-\overline x)}^2}}$,其中$\overline{x_1}$为x1,x2,…,xn的平均数)
 下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )(注:标准差s=$\sqrt{\frac{1}{n}[{{({x_1}-\overline x)}^2}+{{({x_2}-\overline x)}^2}+…+{{({x_n}-\overline x)}^2}}$,其中$\overline{x_1}$为x1,x2,…,xn的平均数)
| A. | $\overline{x_1}$<$\overline{x_2}$,s1<s2 | B. | $\overline{x_1}$<$\overline{x_2}$,s1>s2 | C. | $\overline{x_1}$>$\overline{x_2}$,s1>s2 | D. | $\overline{x_1}$>$\overline{x_2}$,s1<s2 |
19.在△ABC中,角A,B,C所对的边分别为a,b,c,设△ABC的面积为S,下列条件不能推出B≤60°的是( )
| A. | a,b,c成等比数列 | B. | a,b,c成等差数列 | C. | 1+2cos2B≥0 | D. | S≤$\frac{\sqrt{3}}{4}$(a2+c2-b2) |
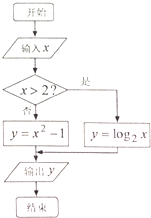 某函数的解析式由如图所示的程序框图给出.
某函数的解析式由如图所示的程序框图给出.