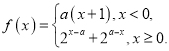题目内容
【题目】一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求恰好得到![]() 分的概率.
分的概率.
【答案】(1)分布列见解析,![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)抛掷5次的得分![]() 可能为
可能为![]() ,且正面向上和反面向上的概率相等,都为
,且正面向上和反面向上的概率相等,都为![]() ,所以得分
,所以得分![]() 的概率为
的概率为![]() ,即可得分布列和数学期望;
,即可得分布列和数学期望;
(2)令![]() 表示恰好得到
表示恰好得到![]() 分的概率,不出现
分的概率,不出现![]() 分的唯一情况是得到
分的唯一情况是得到![]() 分以后再掷出一次反面.,因为“不出现
分以后再掷出一次反面.,因为“不出现![]() 分”的概率是
分”的概率是![]() ,“恰好得到
,“恰好得到![]() 分”的概率是
分”的概率是![]() ,因为“掷一次出现反面”的概率是
,因为“掷一次出现反面”的概率是![]() ,所以有
,所以有![]() ,即
,即![]() ,所以
,所以![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,即求得恰好得到
为公比的等比数列,即求得恰好得到![]() 分的概率.
分的概率.
试题解析:(1)所抛5次得分![]() 的概率为
的概率为![]() ,
,
其分布列如下
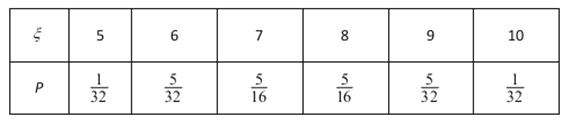
![]()
(2)令![]() 表示恰好得到
表示恰好得到![]() 分的概率,不出现
分的概率,不出现![]() 分的唯一情况是得到
分的唯一情况是得到![]() 分以后再掷出一次反面.
分以后再掷出一次反面.
因为“不出现![]() 分”的概率是
分”的概率是![]() ,“恰好得到
,“恰好得到![]() 分”的概率是
分”的概率是![]() ,
,
因为“掷一次出现反面”的概率是![]() ,所以有
,所以有![]() ,
,
即![]() .
.
于是![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列.
为公比的等比数列.
所以![]() ,即
,即![]() .
.
恰好得到![]() 分的概率是
分的概率是![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)请画出性别与休闲方式的![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.10的前提下,认为休闲方式与性别有关?
附: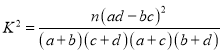 ,
,
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |