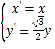题目内容
【题目】已知定义在
上的奇函数
满足
，且
时
，甲，乙，丙，丁四位同学有下列结论：
甲：
；
乙：函数在
上是增函数；
丙：函数关于直线
对称；
丁：若
，则关于
的方程
在
上所有根之和为
其中正确的是（ ）．
A. 甲，乙，丁 B. 乙，丙 C. 甲，乙，丙 D. 甲，丁
【答案】D
【解析】∵
，
是定义在
上的奇函数，
∴
，关于直线
对称，
根据题意，画出的简图，如图所示：
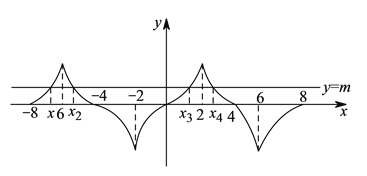
甲：
，故甲同学结论正确；
乙：函数在区间
上是减函数，故乙同学结论错误；
丙：函数关于
中心对称，故丙同学结论错误；
丁：若
由图可知，关于
的方程
在
上有
个根，
设为
，
，
，
，
则
，
，
∴
，
所以丁同学结论正确．
∴甲、乙、丙、丁四位同学结论正确的是甲、丁，
故选
．
点睛:本题考查函数的性质应用以及函数的零点问题,属于中档题目.根据已知函数为奇函数以及函数的周期,可得关于直线对称，结合
时
，画出函数的图象,进而可得函数的单调性,对称性,特殊值以及y=m与y=f(x)的交点情况, 即关于的方程
在
上所有根之和.
【题目】某网店销售某种商品，为了解该商品的月销量
（单位：千件）与月售价
（单位：元/件）之间的关系，对近几年的月销售量
和月销售价
数据进行了统计分析，得到了下面的散点图.
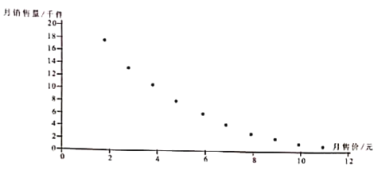
（1）根据散点图判断，
与
哪一个更适宜作为月销量关于月销售价的回归方程类型？（给出判断即可，不需说明理由），并根据判断结果及表中数据，建立关于的回归方程；
（2）利用（1）中的结果回答问题：已知该商品的月销售额为
（单位：千元），当月销售量为何值时，商品的月销售额预报值最大？（月销售额＝月销售量×当月售价）
参考公式、参考数据及说明：
①对一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘法估计分别为
，
.
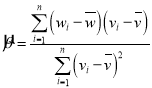②参考数据：
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 | -143.25 | -27.54 |
表中
，
.
③计算时，所有的小数都精确到0.01，如
.
【题目】某快递公司收取快递费用的标准是：重量不超过
的包裹收费
元；重量超过
的包裹，除
收费
元之外，超过
的部分，每超出
（不足
，按
计算）需再收
元.
该公司将近
天，每天揽件数量统计如下：
包裹件数范围 |
|
|
|
|
|
包裹件数 （近似处理） |
|
|
|
|
|
天数 |
|
|
|
|
|
（1）某人打算将
， 
， 
三件礼物随机分成两个包裹寄出，求该人支付的快递费不超过
元的概率；
（2）该公司从收取的每件快递的费用中抽取
元作为前台工作人员的工资和公司利润，剩余的作为其他费用.前台工作人员每人每天揽件不超过
件，工资
元，目前前台有工作人员
人，那么，公司将前台工作人员裁员
人对提高公司利润是否更有利？
