题目内容
8.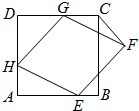 已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.
已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.(1)当DG=2时,求证:∠EHG=90°;
(2)在(1)的条件下,求△FCG的面积;
(3)设DG=x,用含x的代数式表示△FCG的面积.
分析 (1)利用勾股定理可知HG=$2\sqrt{5}$,通过Rt△AHE≌Rt△DGH,计算即得结论;
(2)通过作FM⊥DC,M为垂足,连结GE,利用Rt△DGH≌Rt△CFG,计算即得结论;
(3)通过两直线平行内错角相等可知∠AEH=∠MGF,利用△AHE≌△MFG可知点F到直线CD的距离为定值2,进而计算可得结论.
解答 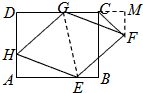 (1)证明:∵在正方形ABCD中,AH=2,
(1)证明:∵在正方形ABCD中,AH=2,
∴DH=4,
又∵DG=2,
∴HG=$\sqrt{{2}^{2}+{4}^{2}}$=$2\sqrt{5}$,
∴菱形EFGH的边长为$2\sqrt{5}$,
易知Rt△AHE≌Rt△DGH,
∴∠DGH+∠AHE=90°,
∴∠EHG=90°;
(2)解:作FM⊥DC,M为垂足,连结GE,
易知Rt△DGH≌Rt△CFG,从而CF=2,
∴S△FCG=$\frac{1}{2}×4×2$=4;
(3)解:连结GE,
∵AB∥CD,∴∠AEG=∠MGE,
∵HE∥GH,∴∠HEG=∠FGE,
∴∠AEH=∠MGF,
在△AHE和△MFG中,∠A=∠M=90°,HE=FG,
∴△AHE≌△MFG,
∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离为定值2,
∴S△FCG=$\frac{1}{2}$×2×(6-x)=6-x.
点评 本题考查函数模型的选择与应用,考查分析问题的、解决问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
19.已知随机变量ξ服从二项分布ξ~B(n,p),且E(ξ)=7,D(ξ)=6,则p等于( )
| A. | $\frac{6}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
17.已知M(-2,0),N(2,0),|PM|-|PN|=3,则动点P的轨迹是( )
| A. | 双曲线 | B. | 双曲线左边一支 | C. | 双曲线右边一支 | D. | 一条射线 |
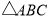 中,
中,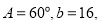 面积
面积 ,则
,则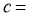
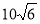 B.7 C.55 D.49
B.7 C.55 D.49 如图,在△ABC中,AD为内角平分线,∠ADC=60°,点E在AD上,满足DE=DB,射线CE交AB于点F,求证:AF•AB+CD•CB=AC2.
如图,在△ABC中,AD为内角平分线,∠ADC=60°,点E在AD上,满足DE=DB,射线CE交AB于点F,求证:AF•AB+CD•CB=AC2.