题目内容
16.已知定义在R上的函数y=f(x)对任意的x都满足f(x+1)=-f(x),当-1≤x<0 时,f(x)=x3,若函数g(x)=f(x)-loga|x|至少6个零点,则a的取值范围是(0,$\frac{1}{5}$]∪(5,+∞).分析 函数g(x)=f(x)-loga|x|的零点个数,即函数y=f(x)与y=log5|x|的交点的个数,由函数图象的变换,分别做出y=f(x)与y=loga|x|的图象,结合图象可得loga5<1 或 loga5≥-1,由此求得a的取值范围.
解答  解:根据题意,函数g(x)=f(x)-loga|x|的零点个数,
解:根据题意,函数g(x)=f(x)-loga|x|的零点个数,
即函数y=f(x)与y=loga|x|的交点的个数;
f(x+2)=f(x),函数f(x)是周期为2的周期函数,
又由当-1<x≤1时,f(x)=x3,
据此可以做出f(x)的图象,
y=loga|x|是偶函数,当x>0时,y=logax,
则当x<0时,y=loga(-x),做出y=loga|x|的图象,
结合图象分析可得:
要使函数y=f(x)与y=loga|x|至少有6个交点,
则 loga5<1 或 loga5≥-1,解得 a≥5,或 0<a≤$\frac{1}{5}$,
故(0,$\frac{1}{5}$]∪(5,+∞),
故答案为:(0,$\frac{1}{5}$]∪(5,+∞)
点评 本题考查函数图象的变化与运用,涉及函数的周期性,对数函数的图象等知识点,关键是作出函数的图象,由此分析两个函数图象交点的个数,属于中档题.

练习册系列答案
相关题目
7.已知a>0,且ab=4,那么a+b的最小值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
1.已知p:(x+3)(x+4)=0,q:x+3=0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知对数函数f(x)过点(2,4),则f($\root{4}{2}$)的值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
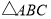 中,
中,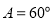 ,且
,且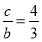 ,则
,则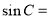 ____________
____________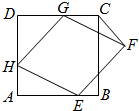 已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.
已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.