题目内容
13.已知f(x)是定义在R上的函数,对任意的x,y∈R都有f(x+y)=f(x)+f(y),且f(-1)=2(1)求f(0),f(-2)的值;
(2)证明:函数f(x)在R上是奇函数.
分析 (1)将x=y=0代入已知等式确定出f(0)的值,把x=-1,y=-1代入已知等式化简,将f(-1)=2代入求出f(-2)的值即可;
(2)令y=-x,得到x+y=0,代入已知等式化简,根据f(0)=0,确定出f(x)的奇偶性即可.
解答 解:(1)令x=y=0,则f(0)=f(0)+f(0)=2f(0),得f(0)=0,
∵f(-1)=2,
∴f(-2)=f(-1)+f(-1)=2f(-1)=4;
(2)令y=-x,即x+y=0,则f(x+y)=f(x)+f(y),即f(0)=f(x)+f(-x),
又∵f(0)=0,
∴f(x)+f(-x)=0,即f(-x)=f(x),
∴函数f(x)在R上是奇函数.
点评 此题考查了抽象函数及其应用,以及函数奇偶性的性质,熟练掌握函数的性质是解本题的关键.

练习册系列答案
相关题目
1.已知p:(x+3)(x+4)=0,q:x+3=0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知对数函数f(x)过点(2,4),则f($\root{4}{2}$)的值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
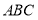 中,内角
中,内角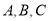 的对边分别为
的对边分别为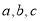 ,且
,且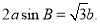
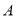 的大小。
的大小。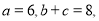 ,求△
,求△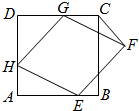 已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.
已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.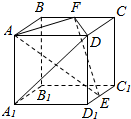 如图所示,在正方体ABCD-A1B1C1D1中,E为棱C1D1的中点,F为棱BC的中点.求证:直线AE⊥直线DA1.
如图所示,在正方体ABCD-A1B1C1D1中,E为棱C1D1的中点,F为棱BC的中点.求证:直线AE⊥直线DA1.