题目内容
8.已知关于x与y之间的一组数据:| x | 2 | 3 | 3 | 6 | 6 |
| y | 2 | 6 | 6 | 10 | 11 |
| A. | (4,7) | B. | (3.5,6.5) | C. | (3.5,7.5) | D. | (5,6) |
分析 要求y与x的线性回归方程为y=bx+a必过的点,需要先求出这组数据的样本中心点,根据所给的表格中的数据,求出横标和纵标的平均值,得到样本中心点,得到结果.
解答 解:∵$\overline{x}$=$\frac{1}{5}$(2+3+3+6+6)=4,$\overline{y}$=$\frac{1}{5}$(2+6+6+10+11)=7,
∴本组数据的样本中心点是(4,7),
∴y与x的线性回归方程为y=bx+a必过点(4,7)
故选:A.
点评 本题考查线性回归方程必过样本中心点,考查学生的计算能力,这是一个基础题.

练习册系列答案
相关题目
3.设F是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的左焦点,P是双曲线右支上的动点,A(1,4),则△PAF周长的最小值为$9+\sqrt{41}$.
13.某地对50人进行运动与性别是否有关测试,其中20名男性中有15名喜欢运动,30名女性中10名喜欢运动.
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)判断喜欢运动是否与性别有关?
参考数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值表:
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)判断喜欢运动是否与性别有关?
参考数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值表:
| P(Χ2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.在△ABC中,若b=2asinB,则A为 ( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$或$\frac{2}{3}π$ | D. | $\frac{5}{6}π$或$\frac{π}{6}$ |
17.二项式(x-1)n的奇数项二项式系数和是64,则n等于( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
18.计算机执行如图的程序段后,输出的结果是( )
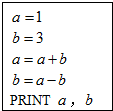
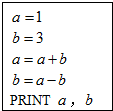
| A. | 1,3 | B. | 4,1 | C. | 4,-2 | D. | 1,-2 |