题目内容
设函数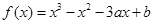 .
.
(1)若曲线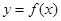 在点
在点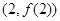 处与直线
处与直线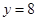 相切,求a,b的值;
相切,求a,b的值;
(2)求函数 的单调区间.
的单调区间.
(1)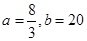 ;(2)
;(2)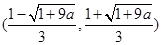 .
.
解析试题分析:(1)首先对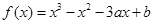 求导,得
求导,得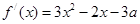 ,利用导数的几何意义求出和切点的意义可得
,利用导数的几何意义求出和切点的意义可得 ,可得
,可得 ,即可解出a,b;(2)根据
,即可解出a,b;(2)根据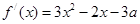 ,就方程
,就方程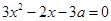 是否有解,利用
是否有解,利用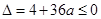 和
和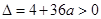 展开讨论,得出单调区间.
展开讨论,得出单调区间.
解:(1)∵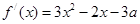
因为曲线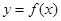 在点
在点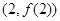 处与直线
处与直线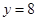 相切,
相切,
∵ ,(2分)即
,(2分)即 解得
解得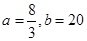 , (6分
, (6分
(2)∵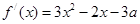
若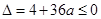 ,即
,即 ,
, ,
,
函数 在(-∞,+∞)上单调递增(8分)
在(-∞,+∞)上单调递增(8分)
若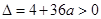 ,即
,即 ,此时
,此时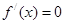 的两个根为
的两个根为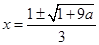
当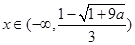 或
或 时
时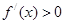
当 时,
时, (11分)
(11分)
故 时,单增区间为当
时,单增区间为当 ,
,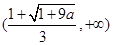
单减区间为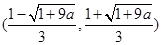 (13分)
(13分)
考点:1.导数的几何意义;2.导数研究函数的单调性.

练习册系列答案
相关题目
 .
. 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和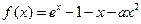 。
。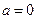 ,求
,求 的单调区间;
的单调区间;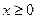 时,
时,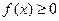 ,求a的取值范围。
,求a的取值范围。 .
. 在点
在点 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值; 时,求
时,求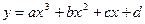 满足下列条件:
满足下列条件: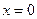 处导数为-1;③在
处导数为-1;③在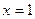 处切线方程为
处切线方程为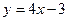 .
.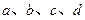 的值;
的值;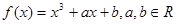 的图象记为E.过点
的图象记为E.过点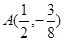 作曲线E的切线,这样的切线有且仅有两条,求
作曲线E的切线,这样的切线有且仅有两条,求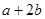 的值.
的值. ,
,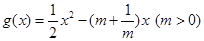 ,且
,且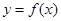 在点
在点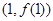 处的切线方程为
处的切线方程为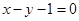 .
.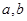 的值;
的值;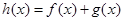 在区间
在区间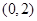 内有且仅有一个极值点,求
内有且仅有一个极值点,求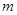 的取值范围;
的取值范围; 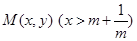 为两曲线
为两曲线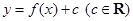 ,
,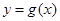 的交点,且两曲线在交点
的交点,且两曲线在交点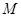 处的切线分别为
处的切线分别为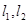 .若取
.若取 ,试判断当直线
,试判断当直线 轴围成等腰三角形时
轴围成等腰三角形时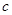 值的个数并说明理由.
值的个数并说明理由.