题目内容
若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点.已知A,b是实数,1和-1是函数f(x)=x3+Ax2+b x的两个极值点.
(1)求A和b的值;
(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点.
(1) 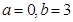 ;(2) 函数g(x)的极值点为
;(2) 函数g(x)的极值点为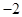 .
.
解析试题分析:(1)极值点时,函数取得极值,对应的导函数的值为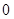 ,先对函数求导得
,先对函数求导得 ,当
,当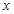 取
取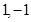 时,导函数值为
时,导函数值为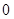 ,得到关于
,得到关于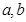 的二元一次方程,解得
的二元一次方程,解得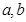 的值;(2)由
的值;(2)由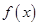 知
知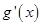 ,令
,令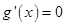 得
得 或
或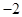 ,两数将定义域分成三个部分,根据极值定义列表判断,可知当
,两数将定义域分成三个部分,根据极值定义列表判断,可知当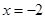 时函数有极小值.
时函数有极小值.
解:(1)因为 ,
,
所以f′(x)=3x2+2Ax+b,且f′(-1)=3-2A+b=0,f′(1)=3+2A+b=0,
解得A=0,b=-3. 4分
经检验,当A=0,b=-3时,1和-1是函数f(x)=x3+Ax2+bx的两个极值点.
综上,所求的A和b的值分别为0,-3. 5分
(2)由(1),知f(x)=x3-3x,所以g′(x)=x3-3x+2=(x-1)2(x+2),
令g′(x)=0,得x=1或x=-2, 7分
当x变化时,g′(x),g(x)的变化情况如下所示:
11分x (-∞,-2) -2 (-2,1) 1 (1,+∞) g′(x) - 0 + 0 + g(x) ↘? 极小值 ↗? 不是极值 ↗
所以x=-2是函数g(x)的极小值点,
即函数g(x)的极值点为-2. 12分
考点:利用导数求函数的极值.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 ,求F(x)=f(x)-g(x)的单调区间;
,求F(x)=f(x)-g(x)的单调区间;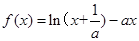 ,其中
,其中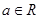 且
且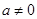 .
.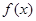 的单调性;
的单调性;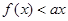 恒成立,求实数
恒成立,求实数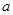 取值范围;
取值范围;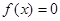 存在两个异号实根
存在两个异号实根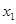 ,
,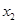 ,求证:
,求证: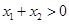
 .
. 的单调区间;
的单调区间; 上是减函数,求实数a的取值范围;
上是减函数,求实数a的取值范围; ,是否存在实数a,当
,是否存在实数a,当 (e是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a的值;若不存在,说明理由.
(e是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a的值;若不存在,说明理由.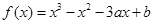 .
.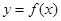 在点
在点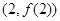 处与直线
处与直线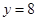 相切,求a,b的值;
相切,求a,b的值; 的单调区间.
的单调区间. ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式; ,其中
,其中 .
. ,使得函数
,使得函数 在
在 上单调递增?若存在,求出的
上单调递增?若存在,求出的 ,求函数的极大值。
,求函数的极大值。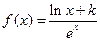 (
(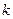 为常数,
为常数,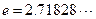 是自然对数的底数),曲线
是自然对数的底数),曲线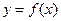 在点
在点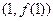 处的切线与
处的切线与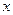 轴平行.
轴平行.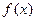 的单调区间;
的单调区间;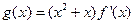 ,其中
,其中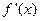 为
为 .
.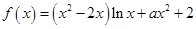 .
.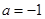 时,求
时,求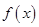 在
在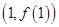 处的切线方程;
处的切线方程; ,
,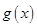 有且仅有一个零点时,求
有且仅有一个零点时,求 的值;
的值;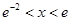 ,
,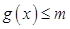 ,求
,求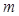 的取值范围.
的取值范围.