题目内容
设复数z=(a2-4sin2θ)+2(1+cosθ)•i,其中a∈R,θ∈(0,π),i为虚数单位.若z是方程x2-2x+2=0的一个根,且z在复平面内对应的点在第一象限,求θ与a的值.
分析:首先求出一元二次方程的虚根,由复数相等的条件列式求解角θ,然后由实部等于1求解a的值.
解答:解:由方程x2-2x+2=0,得
x=
=1±i.
∵z在复平面内对应的点在第一象限,∴z=1+i,
∴1+i=(a2-4sin2θ)+2(1+cosθ)•i,
得
,解得cosθ=-
,
∵θ∈(0,π),∴θ=
,
∴sin2θ=
,∴a2=1+4sin2θ=4,故a=±2.
∴θ=
,a=±2.
x=
2±
| ||
| 2 |
∵z在复平面内对应的点在第一象限,∴z=1+i,
∴1+i=(a2-4sin2θ)+2(1+cosθ)•i,
得
|
| 1 |
| 2 |
∵θ∈(0,π),∴θ=
| 2π |
| 3 |
∴sin2θ=
| 3 |
| 4 |
∴θ=
| 2π |
| 3 |
点评:本题考查了复数的代数表示法及其几何意义,考查了实系数一元二次方程虚根的求法,训练了复数相等条件的应用,考查了由三角函数值求角,是中低档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
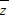 及|
及|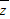 |;
|;