题目内容
下列命题中的真命题为
(1)复平面中满足|z-2|-|z+2|=1的复数z的轨迹是双曲线;
(2)当a在实数集R中变化时,复数z=a2+ai在复平面中的轨迹是一条抛物线;
(3)已知函数y=f(x),x∈R+和数列an=f(n),n∈N,则“数列an=f(n),n∈N递增”是“函数y=f(x),x∈R+递增”的必要非充分条件;
(4)在平面直角坐标系xoy中,将方程g(x,y)=0对应曲线按向量(1,2)平移,得到的新曲线的方程为g(x-1,y-2)=0;
(5)设平面直角坐标系xoy中方程F(x,y)=0表椭圆示一个,则总存在实常数p、q,使得方程F(px,qy)=0表示一个圆.
(2)(3)(4)(5)
(2)(3)(4)(5)
.(1)复平面中满足|z-2|-|z+2|=1的复数z的轨迹是双曲线;
(2)当a在实数集R中变化时,复数z=a2+ai在复平面中的轨迹是一条抛物线;
(3)已知函数y=f(x),x∈R+和数列an=f(n),n∈N,则“数列an=f(n),n∈N递增”是“函数y=f(x),x∈R+递增”的必要非充分条件;
(4)在平面直角坐标系xoy中,将方程g(x,y)=0对应曲线按向量(1,2)平移,得到的新曲线的方程为g(x-1,y-2)=0;
(5)设平面直角坐标系xoy中方程F(x,y)=0表椭圆示一个,则总存在实常数p、q,使得方程F(px,qy)=0表示一个圆.
分析:(1)根据双曲线的定义可得:复数z的轨迹是双曲线的一支.
(2)由题意可得:x=a2,y=a,所以消去参数a可得:y2=x,所以次曲线是一条抛物线.
(3)根据两个函数的定义域之间的关系可得答案.
(4)由“按向量(1,2)平移”与口诀“左加右减,上加下减”之间的关系可得答案.
(5)根据椭圆的方程与圆的方程之间的关系可得(5)正确.
(2)由题意可得:x=a2,y=a,所以消去参数a可得:y2=x,所以次曲线是一条抛物线.
(3)根据两个函数的定义域之间的关系可得答案.
(4)由“按向量(1,2)平移”与口诀“左加右减,上加下减”之间的关系可得答案.
(5)根据椭圆的方程与圆的方程之间的关系可得(5)正确.
解答:解:(1)根据双曲线的定义可得:满足|z-2|-|z+2|=1的复数z的轨迹是双曲线的一支,所以(1)错误.
(2)由复数z=a2+ai可得:x=a2,y=a,所以消去参数a可得:y2=x,所以次曲线是一条抛物线,所以(2)正确.
(3)因为N?R+,并且函数an=f(n)的定义域为n∈N,函数y=f(x)的定义域为x∈R+,所以“函数y=f(x),x∈R+递增”⇒“数列an=f(n),n∈N递增”,但是反之则不成立,所以(3)正确.
(4)按向量(1,2)平移,即为图象先向右平移1个单位,再向上平移2个单位,所以得到的新曲线的方程为g(x-1,y-2)=0,所以(4)正确.
(5)根据椭圆的方程与圆的方程之间的关系可得(5)正确.
故答案为:(2)(3)(4)(5).
(2)由复数z=a2+ai可得:x=a2,y=a,所以消去参数a可得:y2=x,所以次曲线是一条抛物线,所以(2)正确.
(3)因为N?R+,并且函数an=f(n)的定义域为n∈N,函数y=f(x)的定义域为x∈R+,所以“函数y=f(x),x∈R+递增”⇒“数列an=f(n),n∈N递增”,但是反之则不成立,所以(3)正确.
(4)按向量(1,2)平移,即为图象先向右平移1个单位,再向上平移2个单位,所以得到的新曲线的方程为g(x-1,y-2)=0,所以(4)正确.
(5)根据椭圆的方程与圆的方程之间的关系可得(5)正确.
故答案为:(2)(3)(4)(5).
点评:本题主要考查双曲线的定义、椭圆与圆的方程之间的关系,以及函数图象“按向量平移”与口诀“左加右减,上加下减”之间的关系等知识点,此题属于基础题.

练习册系列答案
相关题目
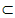 α,则m∥α
α,则m∥α 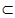 α,则m⊥α
α,则m⊥α 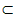 α,m
α,m α,则m∥α
α,则m∥α 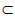 α,m
α,m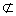 α,则m⊥α
α,则m⊥α