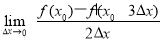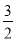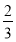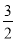Question

设f(x)＝2x3＋ax2＋bx＋1的导数为f′(x)，若函数y＝f′(x)

的图象关于直线x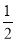＝－对称，且f′(1)＝0.

①求实数a，b的值；②求函数f(x)的极值．

 

Answer 1

①a＝3，b＝－12②－6

【解析】①∵f(x)＝2x3＋ax2＋bx＋1，

∴f′(x)＝6x2＋2ax＋b.

由题意知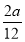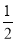，－＝－且6×12＋2a×1＋b＝0，

∴a＝3，b＝－12.

②由①知，f(x)＝2x3＋3x2－12x＋1.

∴f′(x)＝6x2＋6x－12＝6(x＋2)(x－1)

由f′(x)＝0，得x＝1或x＝－2.

由f′(x)>0，得x>1或x<－2，由f′(x)<0，得－2<x<1.

∴f(x)在(－∞，－2)上递增，(－2,1)上递减，(1，＋∞)上递增．

∴当x＝－2时，f(x)取得极大值f(－2)＝21，当x＝1时，f(x)取得极小值f(1)＝－6