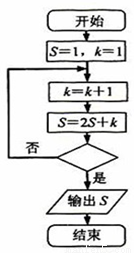
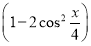题目内容
设函数f(x)=x3+2ax2+bx+a,g(x)=x2-3x+2,其中x∈
R,a,b为常数,已知曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l.
求a,b的值,并求出切线l的方程.
x-y-2=0
【解析】f′(x)=3x2+4ax+b,g′(x)=2x-3,
由于曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线,∴f′(2)=g′(2),f(2)=g(2)=0,∴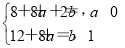 ∴a=-2,b=5.
∴a=-2,b=5.
所以,所求切线的斜率为g′(2)=1,
切线方程为y-0=1(x-2),即x-y-2=0.

练习册系列答案
相关题目