Question

【题目】已知圆C：（x﹣1）2+y2=16，F（﹣1，0），M是圆C上的一个动点，线段MF的垂直平分线与线段MC相交于点P．
（Ⅰ）求点P的轨迹方程；
（Ⅱ）记点P的轨迹为C1 ， A、B是直线x=﹣2上的两点，满足AF⊥BF，曲线C1与过A，B的两条切线（异于x=﹣2）交于点Q，求四边形AQBF面积的取值范围．

Answer 1

【答案】解：（Ⅰ）依题意得圆心C（0，1），半径r=4， ∵线段MF的垂直平分线与线段MC相交于点P，
∴|PF|+|PC|=|PM|+|PC|=CM=4＞|CF|=2．
∴点P的轨迹方程是以C，F为焦点，长轴长为4的椭圆，
即a=2，c=1，则b=22﹣1=3，
∴P的轨迹方程是 ．
（Ⅱ）依题意，直线AF斜率存在且不为零，设为y=k（x+1），
令x=﹣2得A（﹣2，﹣k），同理B（﹣2， ）．
设过点A的切线为y=k1（x+2）﹣k，代入
得 x+4[（2k1﹣k）2﹣3]=0．
由 ，解得 ，
同理k2= = ．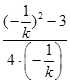
联立方程组： ，解得x=﹣4．
∴ = ，当且仅当k=±1时等号成立，
∴四边形AQBF面积的取值范围是[3，+∞）．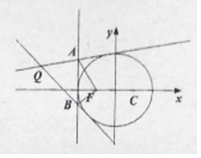

【解析】（I）利用中垂线的性质得出|PF|+|PC|=4，于是P点轨迹为椭圆，根据椭圆定义得出椭圆方程；（II）设AF的斜率为k，用k表示出A，B的坐标，设过A点的切线斜率为k1 ， 联立方程组得出k1和k的关系，同理得出过B点的切线方程，再联立方程组得出Q点坐标，得出四边形面积关于k的解析式，利用不等式得出面积的范围．