题目内容
在等差数列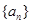 中,
中,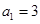 ,其前n项和为
,其前n项和为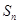 ,等比数列
,等比数列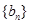 的各项均为正数,
的各项均为正数,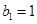 ,公比为q,且
,公比为q,且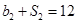 ,
,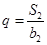 .
.
(1)求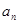 与
与 ;
;
(2)设数列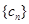 满足
满足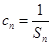 ,求
,求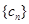 的前n项和
的前n项和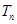 .
.
(1)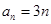 ,
,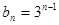 ;(2)
;(2)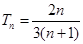 .
.
解析试题分析:本题主要考查等差数列的通项公式、等比数列的通项公式、等差数列的前n项和公式、裂项相消法求和等数学知识,考查学生的计算能力和分析问题的能力.第一问,利用等比数列的通项公式和等差数列的前n项和公式将已知表达式展开,求出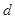 和
和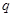 ,从而求出等差数列、等比数列的通项公式;第二问,利用等差数列的前n项和公式先求出
,从而求出等差数列、等比数列的通项公式;第二问,利用等差数列的前n项和公式先求出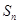 ,得到
,得到 进行裂项,用裂项相消法求数列的前n项和
进行裂项,用裂项相消法求数列的前n项和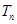 .
.
试题解析:(1)设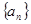 的公差为
的公差为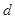 .
.
因为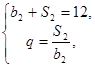 所以
所以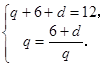 3分
3分
解得 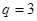 或
或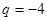 (舍),
(舍),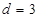
故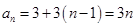 ,
,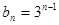 . 6分
. 6分
(2)由(1)可知,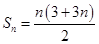 , 7分
, 7分
所以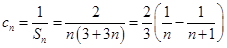 . 9分
. 9分
故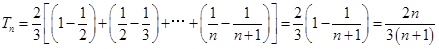 12分
12分
考点:1.等差数列、等比数列的通项公式;2.等差数列的前n项和公式;3.裂项相消法求和.

练习册系列答案
相关题目
 (n∈N*),若Tn+
(n∈N*),若Tn+ <c(c∈Z)恒成立,求c的最小值.
<c(c∈Z)恒成立,求c的最小值.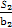 .
. ≤
≤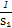 +
+ +…+
+…+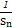 <
< .
.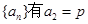 (常数
(常数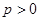 ),其前
),其前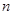 项和为
项和为
 (
(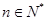 )
)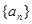 的首项
的首项 ,并判断
,并判断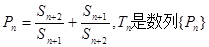 的前n项和,求证:
的前n项和,求证: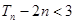
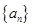 的前
的前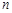 项和为
项和为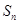 .
.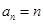 ,数列
,数列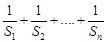 的和.
的和.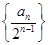 的前n项和.
的前n项和.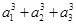 +…+
+…+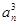 =
=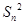 ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.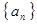 ,满足
,满足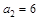 ,
,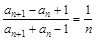
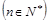 ,
,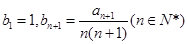 ,求数列
,求数列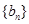 所满足的通项公式;
所满足的通项公式;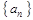 的通项公式;
的通项公式;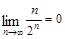 ,设
,设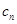 =
=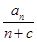
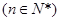 ,常数
,常数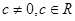 ,若数列
,若数列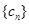 是等差数列,记
是等差数列,记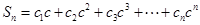 ,求
,求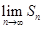 .
.